题目内容
关于x一元二次方程2x(kx-4)-x2+6=0没有实数根,则k的最小整数值是 。
2 【解析】试题分析:先把方程化为一般形式:(2k﹣1)x2﹣8x+6=0,由关于x的一元二次方程2x(kx﹣4)﹣x2+6=0没有实数根,所以2k﹣1≠0且△<0,即解得k>,即可得到k的最小整数值. 把方程化为一般形式:(2k﹣1)x2﹣8x+6=0, ∵原方程为一元二次方程且没有实数根, ∴2k﹣1≠0且△<0,即△=(﹣8)2﹣4×(2k﹣1)×6=88﹣48k<0...
练习册系列答案
相关题目


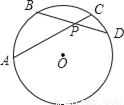
 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.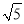 ,cos∠ACF=
,cos∠ACF=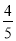 ,求EF的长.
,求EF的长.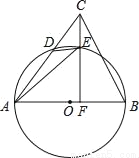

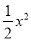 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).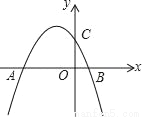
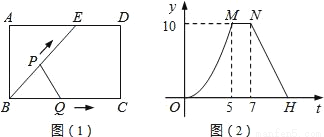
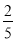 t2;③直线NH的解析式为y=﹣
t2;③直线NH的解析式为y=﹣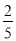 t+27;④若△ABE与△QBP相似,则t=
t+27;④若△ABE与△QBP相似,则t=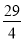 秒,其中正确结论的个数为( )
秒,其中正确结论的个数为( )