题目内容
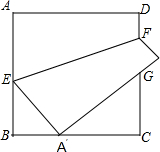 在正方形ABCD中,E、F分别是AB、CD上的点,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,又AD=18,A′B=6,求四边形AEFD的面积.
在正方形ABCD中,E、F分别是AB、CD上的点,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,又AD=18,A′B=6,求四边形AEFD的面积.考点:翻折变换(折叠问题)
专题:计算题
分析:先根据折叠的性质得AE=A′E,FD′=FD,∠EA′G=∠A=90°,∠D′=∠D=90°,设AE=x,则BE=18-x,A′E=x,在Rt△A′BE中,根据勾股定理得62+(18-x)2=x2,解得x=10,则AE=10,BE=8;再证明Rt△A′EB∽Rt△GA′C,利用相似比得CG=9,在Rt△A′CG中,利用勾股定理计算出A′G=15;设FD=y,则FD′=y,FG=18-9-y=9-y,接着证明Rt△GFD′∽Rt△GA′C,利用相似比得到
=
,解得y=4,即DF=4,最后根据梯形的面积公式计算四边形AEFD的面积.
| y |
| 12 |
| 9-y |
| 15 |
解答:解: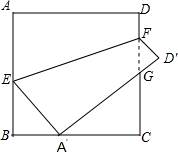 ∵正方形ABCD中,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,
∵正方形ABCD中,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,
∴AE=A′E,FD′=FD,∠EA′G=∠A=90°,∠D′=∠D=90°,
设AE=x,则BE=18-x,A′E=x,
在Rt△A′BE中,∵A′B2+BE2=A′E2,
∴62+(18-x)2=x2,解得x=10,
∴AE=10,BE=8,
∵∠EA′B+∠CA′G=90°,∠EA′B+∠A′EB=90°,
∴∠A′EB=∠CA′G,
∴Rt△A′EB∽Rt△GA′C,
∴
=
,即
=
,解得CG=9,
在Rt△A′CG中,A′G=
=15,
设FD=y,则FD′=y,FG=18-9-y=9-y,
∵∠FGD′=∠A′GC,
∴Rt△GFD′∽Rt△GA′C,
∴
=
,即
=
,解得y=4,
即DF=4,
∴四边形AEFD的面积=
(4+10)×18=126.
 ∵正方形ABCD中,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,
∵正方形ABCD中,把EF上方部分沿EF翻折,若A点正好落在BC上A′处,D点落在正方形外D′处,∴AE=A′E,FD′=FD,∠EA′G=∠A=90°,∠D′=∠D=90°,
设AE=x,则BE=18-x,A′E=x,
在Rt△A′BE中,∵A′B2+BE2=A′E2,
∴62+(18-x)2=x2,解得x=10,
∴AE=10,BE=8,
∵∠EA′B+∠CA′G=90°,∠EA′B+∠A′EB=90°,
∴∠A′EB=∠CA′G,
∴Rt△A′EB∽Rt△GA′C,
∴
| CG |
| A′B |
| A′C |
| BE |
| CG |
| 6 |
| 18-6 |
| 8 |
在Rt△A′CG中,A′G=
| A′C2+CG2 |
设FD=y,则FD′=y,FG=18-9-y=9-y,
∵∠FGD′=∠A′GC,
∴Rt△GFD′∽Rt△GA′C,
∴
| FD′ |
| A′C |
| FG |
| A′G |
| y |
| 12 |
| 9-y |
| 15 |
即DF=4,
∴四边形AEFD的面积=
| 1 |
| 2 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质、勾股定理和相似三角形的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两个有理数之积是0,那么这两个有理数( )
| A、至少有一个是0 | B、都是0 |
| C、互为倒数 | D、互为相反数 |
如果P(a+b,ab)在第二象限,那么点Q(a,-b)在第( )象限.
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若m是正整数,则
+
的值( )
| 1m |
| 2 |
| (-1)m |
| 2 |
| A、是0 | B、是1或-1 |
| C、是-1或0 | D、是1或0 |
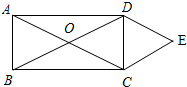 如图在矩形ABCD中,对角线AC、BD相交于点O,且DE∥AC,CE∥BD,试判断四边形OCED的形状.
如图在矩形ABCD中,对角线AC、BD相交于点O,且DE∥AC,CE∥BD,试判断四边形OCED的形状.