题目内容
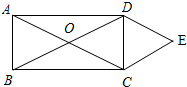如图在矩形ABCD中，对角线AC、BD相交于点O，且DE∥AC，CE∥BD，试判断四边形OCED的形状．考点：菱形的判定
专题：
分析：首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形，然后根据矩形的性质：矩形的对角线相等且互相平分，可得OC=OD，由此可判定四边形OCED是菱形．
解答：证明：四边形OCED是菱形．
∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
又在矩形ABCD中，OC=OD，
∴四边形OCED是菱形．
∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
又在矩形ABCD中，OC=OD，
∴四边形OCED是菱形．
点评：本题主要考查矩形的性质，平行四边形、菱形的判定；
菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
练习册系列答案
相关题目
将△ABC的三个顶点的纵坐标不变，横坐标乘以-l后得到△DEF，则△DEF（ ）
| A、与△ABC关于x轴对称 |
| B、与△ABC关于y轴对称 |
| C、与△ABC关于原点对称 |
| D、向x轴的负方向平移了一个单位 |
若
+
=
，则用u、v表示f的式子应该是（ ）
| 1 |
| u |
| 1 |
| v |
| 1 |
| f |
A、
| ||
B、
| ||
C、
| ||
D、
|
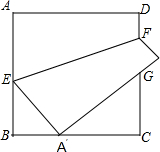在正方形ABCD中，E、F分别是AB、CD上的点，把EF上方部分沿EF翻折，若A点正好落在BC上A′处，D点落在正方形外D′处，又AD=18，A′B=6，求四边形AEFD的面积．