Question

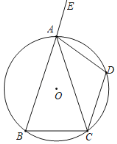
【题目】如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，D为弧AC的中点，E是BA延长线上一点，∠DAE＝105°．

（1）求∠CAD的度数；

（2）若⊙O的半径为4，求弧BC的长．

Answer 1

【答案】（1）∠CAD＝35°；（2）．

【解析】

(1)由AB=AC，得到=，求得∠ABC=∠ACB，推出∠CAD=∠ACD，得到∠ACB=2∠ACD，于是得到结论；

(2)根据平角的定义得到∠BAC=40°，连接OB，OC，根据圆周角定理得到∠BOC=80°，根据弧长公式即可得到结论．

(1)∵AB=AC，

∴=，

∴∠ABC=∠ACB，

∵D为的中点，

∴=，

∴∠CAD=∠ACD，

∴=2，

∴∠ACB=2∠ACD，

又∵∠DAE=105°，

∴∠BCD=105°，

∴∠ACD=×105°=35°，

∴∠CAD=35°；

(2)∵∠DAE=105°，∠CAD=35°，

∴∠BAC=180°-∠DAE-∠CAD=40°，

连接OB，OC，

∴∠BOC=80°，

∴弧BC的长==．