题目内容
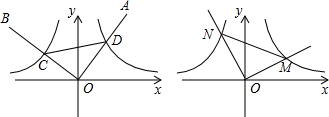
如图,射线OA与反比例函数y1=
(x>0)图象交于点D(1,2),射线OB与反比例函数y2=-
(x<0)的图象交于点C,且CD∥x轴.
(1)求∠AOB的度数;
(2)如图,将∠AOB绕着点O旋转一定的角度,射线OA,OB分别交反比例函数y1,y2的图象于M,N两点,在旋转过程中,∠OMN的度数是否会发生变化?请说明理由.
| k1 |
| x |
| 8 |
| x |
(1)求∠AOB的度数;
(2)如图,将∠AOB绕着点O旋转一定的角度,射线OA,OB分别交反比例函数y1,y2的图象于M,N两点,在旋转过程中,∠OMN的度数是否会发生变化?请说明理由.

考点:反比例函数综合题
专题:
分析:(1)将点D的坐标代入y1,求出k1的值,然后根据CD∥x轴,求出点C的坐标,求得CD,OD,OC的长,由勾股定理的逆定理,即可证得△AOB是直角三角形;
(2)首先作MF⊥x轴于F,NE⊥x轴于E,设M(a,
),N(b,-
),则MF=
,OF=a,OE=-b,NE=-
,易证得Rt△ONE∽Rt△MOF,然后由相似三角形的对应边成比例,求得ON:OM的值,即可求得答案.
(2)首先作MF⊥x轴于F,NE⊥x轴于E,设M(a,
| 2 |
| a |
| 8 |
| b |
| 2 |
| a |
| 8 |
| b |
解答:解:(1)将点D的坐标代入y1得k1=1,
则y1=
,
∵CD∥x轴,
∴点C的纵坐标为2,
则点C的横坐标为:-8÷2=-4,
即C(-4,2),
∴CD=5,OD=
=
,OC=
=2
,
∴OA2+OB2=5+20=AB2,
∴∠COD=90°,
即∠AOB=90°;
(2)不变化.理由如下:
作MF⊥x轴于F,NE⊥x轴于E,如图所示,
设M(a,
),N(b,-
),
则MF=
,OF=a,OE=-b,NE=-
,
∵∠AOB绕着点O旋转一定的角度,使∠AOB的两边分别交反比例函数y1、y2的图象于点M、N,
∴∠MON=90°,
∴∠NOE+∠MOF=90°,
而∠NOE+∠ONE=90°,
∴∠ONE=∠MOF,
∴Rt△ONE∽Rt△MOF,
∴
=
=
,
即
=
,
∴a2b2=16,
∵ab<0,
∴ab=-4,
∴
=-
=-
=2,
在Rt△OMN中,tan∠NMO=
=2,
∴在旋转的过程中,∠OMN的度数不变化.

则y1=
| 2 |
| x |
∵CD∥x轴,
∴点C的纵坐标为2,
则点C的横坐标为:-8÷2=-4,
即C(-4,2),
∴CD=5,OD=
| 1+22 |
| 5 |
| 22+42 |
| 5 |
∴OA2+OB2=5+20=AB2,
∴∠COD=90°,
即∠AOB=90°;
(2)不变化.理由如下:
作MF⊥x轴于F,NE⊥x轴于E,如图所示,
设M(a,
| 2 |
| a |
| 8 |
| b |
则MF=
| 2 |
| a |
| 8 |
| b |
∵∠AOB绕着点O旋转一定的角度,使∠AOB的两边分别交反比例函数y1、y2的图象于点M、N,
∴∠MON=90°,
∴∠NOE+∠MOF=90°,
而∠NOE+∠ONE=90°,
∴∠ONE=∠MOF,
∴Rt△ONE∽Rt△MOF,
∴
| NE |
| OF |
| OE |
| MF |
| ON |
| OM |
即
-
| ||
| a |
-
| ||
| a |
∴a2b2=16,
∵ab<0,
∴ab=-4,
∴
| ON |
| OM |
| ab |
| 2 |
| -4 |
| 2 |
在Rt△OMN中,tan∠NMO=
| ON |
| OM |
∴在旋转的过程中,∠OMN的度数不变化.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义和平行四边形的性质;会利用相似比进行计算.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
相反数为3的数是( )
| A、-3 | ||
| B、3 | ||
| C、9 | ||
D、
|
 如图,在⊙O中,弦BC,BD关于直径AB所在直线对称.E为半径OC上一点,OC=3OE,连接AE并延长交⊙O于点F,连接DF交BC于点M.
如图,在⊙O中,弦BC,BD关于直径AB所在直线对称.E为半径OC上一点,OC=3OE,连接AE并延长交⊙O于点F,连接DF交BC于点M. P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为
P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为 将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.
将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.