题目内容

11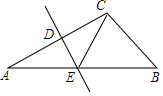．如图，△ABC中，AB=10，BC=6，边AC的垂直平分线分别交AB、AC于点E、D，则△BCE的周长为16．

分析 根据中垂线的性质得出EA=EC，从而由△BCE的周长为EC+EB+BC=EA+EB+BC=AB+BC可得答案．

解答 解：∵DE垂直平分AC，
∴EA=EC，
∴△BCE的周长为EC+EB+BC=EA+EB+BC=AB+BC=16，
故答案为：16．

点评 本题考查的是线段垂直平分线的性质，即线段的垂直平分线上的点到线段的两个端点的距离相等．

练习册系列答案
相关题目
1．在△ABC中，∠B=30°，AB=4，AC=2，则BC=2$\sqrt{3}$．
2．下列图形中，棱锥是（　　）
A．B．C．D．
19．已知一个多项式与3x2+9x的和等于3x2+4x-1，则这个多项式是（　　）
A．13x-1B．6x2+13x-1C．5x+1D．-5x-1
6．下列各数中：$\frac{22}{7}$，0，π，$\root{3}{-8}$，$\root{3}{9}$，0.32，（$\sqrt{3}$）0，$\frac{\sqrt{3}}{4}$，0.1010010001…中，无理数个数有（　　）
A．3个B．4个C．5个D．6个
16．现有三张分别标有数字1、2、6的卡片，它们除了数字外完全相同，把卡片背面朝上洗匀，从中任意抽取一张，将上面的数字记为a（不放回），再从中任意抽取一张，将上面的数字记为b，这样的数字a，b能使关于x的一元二次方程x2-2（a-3）x-b2+9=0有两个正根的概率为$\frac{1}{6}$．
3．小明用正多边形铺设地面，他剪出下列四种正多边形，其中不能单独铺满地面的是（　　）
A．正三角形B．正方形C．正六边形D．正八边形
20．在RtABC中，∠C=90°，AB=13，AC=12，BC=5，则下列各式中正确的是（　　）
A．sinA=$\frac{12}{5}$B．cosA=$\frac{12}{13}$C．tanA=$\frac{12}{5}$D．tanA=$\frac{12}{13}$
1．如图，直线y=$\frac{1}{2}$x+2分别交x、y轴于点A、C，点P是该直线与反比例函数y=$\frac{k}{x}$在第一象限内的交点，PB⊥x轴，B为垂足，S△ABP=9．
（1）直接写出点A的坐标（-4，0）；点C的坐标（0，2）；点P的坐标（2，3）；
（2）若Q为反比例函数在第一象限图象上的点（点Q与点P不重合），且Q点的横坐标为6，在x轴上确定一点M，使MP+MQ最小，并直接写出点M的坐标；
（3）设点R与点P在同一个反比例函数的图象上，且点R在直线PB的右侧，作RT⊥x轴，T为垂足，当△BRT与△AOC相似时，求点R的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网