题目内容
7.用完全一样的火柴棍按如图所示的方法拼成“金鱼”形状的图形,则按照这样的方法拼成第4个图形需要火柴棍30根,拼成第n个图形(n为正整数)需要火柴棍7n+2根(用含n的代数式表示).
分析 观察给出的3个例图,搭1条金鱼需要火柴9根,搭2条金鱼需要16根,搭3条金鱼需要火柴23根,即发现了每多搭1条金鱼,需要多用7根火柴…由此规律解决问题即可.
解答 解:第1个图形需要火柴9根,
第2个图形需要9+7=16根,
第3个图形需要火柴16+7=23根,
第4个图形需要23+7=30根,
…
第n个图形需要火柴9+7(n-1)=7n+2,
故答案为:30,7n+2.
点评 此题考查图形的规律性,从简单图形入手,找到火柴棒根数的变化规律,然后猜想第n条金鱼所需要的火柴棒的根数.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
2.下列图形中,棱锥是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
19.已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是( )
| A. | 13x-1 | B. | 6x2+13x-1 | C. | 5x+1 | D. | -5x-1 |
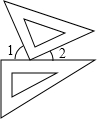 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,设∠1=x°,∠2=y°,先根据题意列出二元一次方程组,再求解.
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,设∠1=x°,∠2=y°,先根据题意列出二元一次方程组,再求解.