题目内容
 如图,AB,CD,EF相交于点O,且它们被O平分,则图中全等的三角形有
如图,AB,CD,EF相交于点O,且它们被O平分,则图中全等的三角形有
- A.1对
- B.2对
- C.3对
- D.4对
C
分析:根据对顶角相等和线段的中点的定义,运用SAS可得△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF,共3对.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
解答:∵AB,CD,EF相交于点O,且它们被O平分,
∴OA=OB,OC=DO,OE=OF,
而∠AOE=∠BOF,∠BOD=∠AOC,∠COE=∠BOF,
∴△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF.
故选C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
分析:根据对顶角相等和线段的中点的定义,运用SAS可得△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF,共3对.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
解答:∵AB,CD,EF相交于点O,且它们被O平分,
∴OA=OB,OC=DO,OE=OF,
而∠AOE=∠BOF,∠BOD=∠AOC,∠COE=∠BOF,
∴△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF.
故选C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
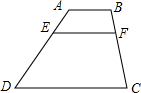 如图,AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为
如图,AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为 17、如图,AB,CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是
17、如图,AB,CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是 15、如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P=
15、如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P=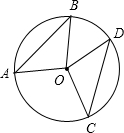 如图,AB、CD是⊙O的两条弦,如果∠AOB=∠COD,那么
如图,AB、CD是⊙O的两条弦,如果∠AOB=∠COD,那么 如图,AB与CD相交于点E,AE=CE,如果根据“SAS”可以判定△ADE≌△CBE,那么只需要补充一个条件
如图,AB与CD相交于点E,AE=CE,如果根据“SAS”可以判定△ADE≌△CBE,那么只需要补充一个条件