题目内容
15、如图，AB、CD是⊙O的两条互相垂直的弦，圆心角∠AOC=130°，AD，CB的延长线相交于P，∠P=40
度．分析：运用同弧所对的圆周角是圆心角的2倍得出∠ADC=∠ABC=65°，再求∠DCB，从而求出∠P．
解答：解：设AB与CD交于点E，∵AB⊥CD，∴∠AED=∠CEB=90°，∵圆心角∠AOC=130°，
∴∠ADC=∠ABC=65°，∴∠BAD=∠DCB=90°-65°=25°，∵∠ADC=∠P+∠DCP，
∴∠P=65°-25°=40°．
∴∠ADC=∠ABC=65°，∴∠BAD=∠DCB=90°-65°=25°，∵∠ADC=∠P+∠DCP，
∴∠P=65°-25°=40°．
点评：本题利用了直角三角形的性质和三角形的外角与内角的关系及圆周角定理求解．
练习册系列答案
相关题目
21、如图，AB、CD是⊙O的弦，∠A=∠C．求证：AB=CD．
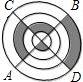如图，AB、CD是水平放置的轮盘（俯视图）上两条互相垂直的直径，一个小钢球在轮盘上自由滚动，该小钢球最终停在阴影区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•泰安）如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
（2013•盘锦）如图，AB，CD是⊙O的直径，点E在AB延长线上，FE⊥AB，BE=EF=2，FE的延长线交CD延长线于点G，DG=GE=3，连接FD．
如图，AB，CD是⊙O的两条弦，且AB=CD，点M是