题目内容
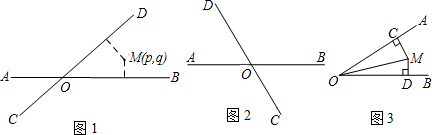
1.定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.(1)“距离坐标”为(1,0)点有2个;
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,$\sqrt{3}$),且∠AOB=30°,求OM的长.
分析 (1)根据两条相交直线把平面分成四部分,在每一个部分内都存在一个满足要求的距离坐标解答;
(2)过M作MN⊥AB于N,根据已知得出OM=n,MN=m,求出∠NOM=30°,根据锐角三角函数得出cos30°=$\frac{ON}{OM}=\frac{p}{q}$,求出即可;
(3)分别作点M关于OA、OB的对称点E、F,连接EF、OE、OF、EM、FM,根据直角三角形的性质解答即可.
解答 解:(1)“距离坐标”为(1,0)点有2个;
故答案为:2;
(2)过M作MN⊥AB于N,如图2:
∵直线l⊥CD于O,∠BOD=120°,
∴∠MON=30°.
∵ON=p,OM=q,
∴$p=\frac{\sqrt{3}}{2}q$;
(3)分别作点M关于OA、OB的对称点E、F,连接EF、OE、OF、EM、FM,如图3:
∴△OEC≌△OMC,△OFD≌△OMD.
∴∠AOM=∠AOE,∠BOM=∠BOF,OM=OE=OF,
∴∠EOF=60°,
∴OM=OE=OF=EF,
∵MD=1,MC=$\sqrt{3}$,
∴MF=2,ME=$2\sqrt{3}$,
∵∠AOB=30°,
∴∠CMD=150°,
过F做FG⊥CM,交CM延长线于G,如图2:
∴∠FMG=30°.
在Rt△FMG中,FG=1,MG=$\sqrt{3}$,
在Rt△EFG中,FG=1,EG=$3\sqrt{3}$,
∴EF=$\sqrt{(3\sqrt{3})^{2}+1}=2\sqrt{7}$,
∴OM=$2\sqrt{7}$.
点评 本题考查了几何变换问题,关键是根据锐角三角函数值,含30度角的直角三角形的应用,主要考查学生的动手操作能力和计算能力,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
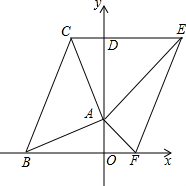 如图,经过点A作三条直线AB、AE、AF,他们的解析式分别是y=k(x+4),y=x+b和y=b-x,直线AB,AF分别和x轴交于B,F,再经过点A作AB的垂线AC,经过点D(0,4+4k)且和y轴垂直的直线交直线AC于点C,和直线AE交于点E.
如图,经过点A作三条直线AB、AE、AF,他们的解析式分别是y=k(x+4),y=x+b和y=b-x,直线AB,AF分别和x轴交于B,F,再经过点A作AB的垂线AC,经过点D(0,4+4k)且和y轴垂直的直线交直线AC于点C,和直线AE交于点E.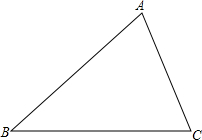 尺规作图:(不写作法,保留作图痕迹)
尺规作图:(不写作法,保留作图痕迹)