题目内容
如图:已知直线y= 与双曲线y=
与双曲线y= 交于A、B两点,且点A的横坐标为4
交于A、B两点,且点A的横坐标为4

⑴求k的值;
⑵若双曲线y= 上的一点C的纵坐标为8,求△AOC的面积?
上的一点C的纵坐标为8,求△AOC的面积?
 与双曲线y=
与双曲线y= 交于A、B两点,且点A的横坐标为4
交于A、B两点,且点A的横坐标为4
⑴求k的值;
⑵若双曲线y=
 上的一点C的纵坐标为8,求△AOC的面积?
上的一点C的纵坐标为8,求△AOC的面积?⑴k=8 ⑵S△AOC=15
(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义可知S△COE=S△AOF,所以S梯形CEFA=S△COA=15.
解:(1)∵点A横坐标为4,
∴当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y= x与双曲线y=
x与双曲线y= (k>0)的交点,
(k>0)的交点,
∴k=4×2=8.(3分)
(2)如图,
过点C、A分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y= 上,当y=8时,x=1.
上,当y=8时,x=1.
∴点C的坐标为(1,8).
∵点C、A都在双曲线y= 上,
上,
∴S△COE=S△AOF=4.
∴S△COE+S梯形CEFA=S△COA+S△AOF.
∴S△COA=S梯形CEFA.(6分)
∵S梯形CEFA= ×(2+8)×3=15,
×(2+8)×3=15,
∴S△COA=15.(8分)
(2)根据k的几何意义可知S△COE=S△AOF,所以S梯形CEFA=S△COA=15.
解:(1)∵点A横坐标为4,
∴当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y=
 x与双曲线y=
x与双曲线y= (k>0)的交点,
(k>0)的交点,∴k=4×2=8.(3分)
(2)如图,

过点C、A分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y=
 上,当y=8时,x=1.
上,当y=8时,x=1.∴点C的坐标为(1,8).
∵点C、A都在双曲线y=
 上,
上,∴S△COE=S△AOF=4.
∴S△COE+S梯形CEFA=S△COA+S△AOF.
∴S△COA=S梯形CEFA.(6分)
∵S梯形CEFA=
 ×(2+8)×3=15,
×(2+8)×3=15,∴S△COA=15.(8分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图像经过第二、四象限,则
的图像经过第二、四象限,则 的取值范围是( )
的取值范围是( )


 (k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.
(k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.  以加热的饮水机,该饮水机的工作程序是:放满水后,
以加热的饮水机,该饮水机的工作程序是:放满水后,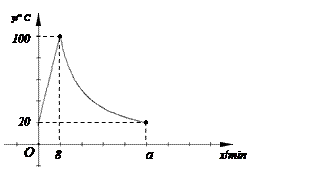
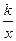 (x > 0)的图象
(x > 0)的图象 上,矩形ABCD的边BC在x轴上,E是对角线BD中点,函数y =
上,矩形ABCD的边BC在x轴上,E是对角线BD中点,函数y =

 ABD=45°, 求 m
ABD=45°, 求 m 的值
的值 上,则下列点一定在该曲线上的是( )
上,则下列点一定在该曲线上的是( ) 的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=
的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=
 与点
与点
 都在反比例函数
都在反比例函数
 的图象上,则m与n的关系是
的图象上,则m与n的关系是 


 ),(2,
),(2, ),(3,
),(3, )在反比例函数
)在反比例函数 的图像上. 下列结论中正确的是
的图像上. 下列结论中正确的是


