题目内容
19.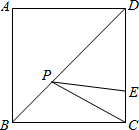 如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是5.
如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是5.
分析 连接AC、AE,由正方形的性质可知A、C关于直线BD对称,则AE的长即为PC+PE的最小值,再根据勾股定理求出AE的长即可.
解答  解:连接AC、AE,
解:连接AC、AE,
∵四边形ABCD是正方形,
∴A、C关于直线BD对称,
∴AE的长即为PC+PE的最小值,
∵CD=4,CE=1,
∴DE=3,
在Rt△ADE中,
∵AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴PC+PE的最小值为5.
故答案为:5.
点评 本题考查的是轴对称-最短路线问题及正方形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
9. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
10.下列计算正确的是( )
| A. | 2a×3a=5a | B. | (-2a)3=-6a3 | C. | 6a÷2a=3a | D. | (-a3)2=a6 |
7.下列运算正确的是( )
| A. | (a3)2=a5 | B. | a2•a3=a5 | C. | a6÷a2=a3 | D. | 3a2-2a2=1 |
4.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
| A. | 22 | B. | 20 | C. | 22或20 | D. | 18 |
15.一次函数y=kx-k(k>0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
16.点P(2,-6)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
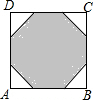 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.
如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.