题目内容
9. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
分析 连接OA,OB,求出圆心角∠AOB的度数,再利用弧长公式解答即可.
解答 解:连接OA,OB,
∵多边形ABCDEF为正六边形,
∴∠AOB=360°×$\frac{1}{6}$=60°,
∴$\widehat{AB}$的长=$\frac{60π×1}{180}$=$\frac{π}{3}$,
故选B.
点评 本题考查了正多边形和圆的位置关系以及弧长公式的运用,此题将扇形的弧长公式与多边形的性质相结合,构思巧妙,利用了正六边形的性质,是一道好题.

练习册系列答案
相关题目
20.在下面艺术汉字中,可以看成轴对称图形的字是( )
| A. |  | B. |  | C. |  | D. |  |
4.将一次函数y=2x-b(b为常数)的图象位于x轴上方的部分沿x轴翻折后,得到的折线是函数y=-|2x-b|(b为常数)的图象.若该图象在直线y=-4上方的点的横坐标x都满足0<x<5.则b的取值范围是( )
| A. | b≥-6 | B. | b≤4 | C. | -6≤b≤-4 | D. | 4≤b≤6 |
14.下列各题计算结果为2a2的是( )
| A. | a6÷a3 | B. | 2a•a | C. | (-2a)2 | D. | (a2)2 |
1.李阿姨从家步行20分钟到离家900米的便利店买东西,用10分钟买完东西,立即步行15分钟回到家中.下列图象中,能表示李阿姨离开家的距离s(米)与她步行时间t(分)之间关系的是( )
| A. |  | B. |  | C. |  | D. |  |
18.随着经济发展,人民的生活水平不断提高,旅游业快速增长,2016年国民出境旅游超过120 000 000人次,将120 000 000用科学记数法表示为( )
| A. | 1.2×109 | B. | 12×107 | C. | 0.12×109 | D. | 1.2×108 |
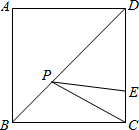 如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是5.
如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是5.