题目内容
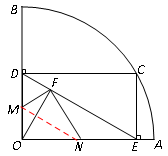
如图,扇形OAB的半径为4,圆心角∠AOB=90°,点C是 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
(1)当 时,求
时,求 的值;
的值;
(2)设OM=x,ON=y,当 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.

 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.(1)当
 时,求
时,求 的值;
的值;(2)设OM=x,ON=y,当
 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.

(1) ;(2)
;(2) ;(3)
;(3) 或
或 .
.
 ;(2)
;(2) ;(3)
;(3) 或
或 .
.试题分析:(1)由△MFO∽△NFE和
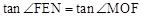 ,根据相似三角形的判定和性质,锐角三角函数定义, 即可求得结果.
,根据相似三角形的判定和性质,锐角三角函数定义, 即可求得结果.(2)由△MFO∽△NFE和△ODF∽△EOF可得
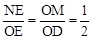 ,即
,即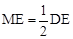 ,从而根据勾股定理可得出
,从而根据勾股定理可得出 ,即
,即 .
.(3)分
 或
或 两种情况讨论即可.
两种情况讨论即可.(1)由题意,得:∠MOF+∠FOE=90°,∠FEN+∠FOE="90°" , ∴∠MOF=∠FEN .
由题意,得:∠MFO+∠OFN=90°,∠EFN+∠OFN="90°" , ∴∠MFO=∠NFE.
∴△MFO∽△NFE.∴
 .
.由∠FEN=∠MOF可得:
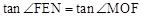 , ∴
, ∴ , ∴
, ∴ .
.(2)∵△MFO∽△NFE , ∴
 .
.又易证得:△ODF∽△EOF , ∴
 .
.∴
 , ∴
, ∴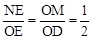 .
. 如图,连接MN,则
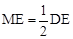 .
.由题意,得四边形ODCE为矩形,∴DE="OC=4" .∴MN=2.
在Rt△MON中,
 ,即
,即 .
.∴y关于x 的函数解析式为
 .
.
(3)由题意,可得: OE=2y,CE=OD=2x.
∴由题意,可得:
 , ∴
, ∴ .
.∵又
 ,∴
,∴ ,∴
,∴ .
.由题意,可得:∠NOF=∠FEC ,
∴由△ECF与△OFN相似,可得:
 或
或 .
.当
 时,
时, ,∴
,∴ .
.又
 ,∴
,∴ ,解得:
,解得: (舍去).
(舍去).∴
 .
.②当
 时,
时, ,∴
,∴ ,
,又
 ,∴
,∴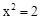 ,∴解得:
,∴解得: (舍去)
(舍去)∴
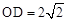 .
.综上所述,OD=
 或
或 .
.
练习册系列答案
相关题目

 上确定点D,使CD与
上确定点D,使CD与
 ,
, );
);

 )
)
 ,即用a、b、
,即用a、b、

 ︱+(
︱+( -cosB)2=0,则∠C=___________________.
-cosB)2=0,则∠C=___________________.