题目内容
5.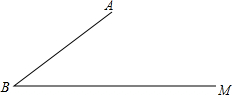 如图,已知∠ABM=37°,AB=20,C是射线BM上一点.
如图,已知∠ABM=37°,AB=20,C是射线BM上一点.(1)求点A到BM的距离;
(2)在下列条件中,可以唯一确定BC长的是②③;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=$\frac{12}{5}$;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
分析 (1)作AD⊥BC,由AD=AB•sinB可得;
(2)根据AC的长大于点A到直线的距离可判断①,利用AAS可判断②,根据平行线间的距离可判断③;
(3)②:先求得BD=AB•cosB=16,再求得CD=$\frac{AD}{tan∠ACB}$=5即可;③:作CE⊥AB,根据面积得出CE=12.6,由BC=$\frac{CE}{sinB}$可得答案.
解答 解:(1)作AD⊥BC于D,则∠ADB=90°.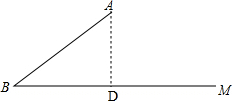
在Rt△ABD中,∵∠ADB=90°,
∴AD=AB•sinB=12;
(2)①以点A为圆心、13为半径画圆,与BM有两个交点,不唯一;
②由tan∠ACB=$\frac{12}{5}$知∠ACB的大小确定,在△ABC中,∠ACB、∠B及AB确定,此时的三角形唯一;
③AB的长度和三角形的面积均确定,则点C到AC的距离即可确定,则BM上的点C是唯一的;
故答案为:②③;
(3)方案一:选②,
由(1)得,AD=12,BD=AB•cosB=16,
在Rt△ACD中,∵∠ADC=90°,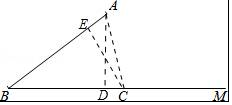
∴CD=$\frac{AD}{tan∠ACB}$=5,
∴BC=BD+CD=21.
方案二:选③,
作CE⊥AB于E,则∠BEC=90°,
由S△ABC=$\frac{1}{2}$AB•CE得CE=12.6,
在Rt△BEC中,
∵∠BEC=90°,
∴BC=$\frac{CE}{sinB}$=21.
点评 本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.

练习册系列答案
相关题目
15.在平面内将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,下列关于平移的说法正确的是( )
| A. | 平移不改变图形的大小,只改变图形的形状 | |
| B. | 平移不改变图形的位置,只改变图形的大小 | |
| C. | 平移不改变图形的形状,只改变图形的大小 | |
| D. | 平移不改变图形的大小与形状,只改变图形的位置 |

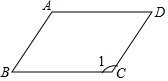 在四边形ABCD中,已知∠B=60°,∠1=120°,AB与CD平行吗?AD与BC平行吗?
在四边形ABCD中,已知∠B=60°,∠1=120°,AB与CD平行吗?AD与BC平行吗?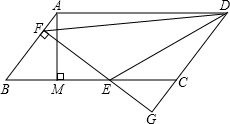 如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.
如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.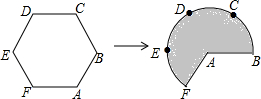 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )