题目内容
10.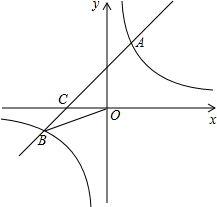 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{1}{2}$.(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
分析 (1)过B作x轴的垂线,垂足为D,求出BD=2,根据tan∠BOC=$\frac{1}{2}$求出OD=4,得出B的坐标,把B的坐标代入y=$\frac{k}{x}$即可求出反比例函数的解析式,求出A的坐标,把A、B的坐标代入一次函数的解析式,即可求出解析式;
(2)求出CO=2,根据三角形面积公式求出即可;
(3)设P点的坐标为P(a,0)根据S△PAC=S△BOC得出$\frac{1}{2}$PC×4=2,求出PC即可.
解答 解:(1)过B作x轴的垂线,垂足为D,
∵B的坐标为(n,-2),
∴BD=2,
∵tan∠BOC=$\frac{1}{2}$,
∴OD=4,
∴B的坐标为(-4,-2)
把B(-4,-2)代入y=$\frac{k}{x}$得:k=8,
∴反比例函数为y=$\frac{8}{x}$,
把A(2,m)代入y=$\frac{8}{x}$得:m=4,
∴A(2,4),
把A(2,4)和B(-4,-2)代入y=ax+b得:$\left\{\begin{array}{l}{2a+b=4}\\{-4a+b=-2}\end{array}\right.$
解得:a=1,b=2,
∴一次函数的解析式为:y=x+2;
(2)在y=x+2中,令y=0,得x=-2,
∴CO=2,
∴S△BOC=$\frac{1}{2}$CO•BD=$\frac{1}{2}$×2×2=2;
(3)设P点的坐标为P(a,0)
则由S△PAC=S△BOC得:$\frac{1}{2}$PC×4=2,
∴PC=1,
即||a+2|=1,
解得:a=-3或a=-1,
即P的坐标为(-3,0)或(-1,0).
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式,三角形的面积,函数的图象的应用,解此题的关键是能综合运用知识点进行计算,数形结合思想的应用,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4a2-2a2=2 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | (3a)2=6a2 |
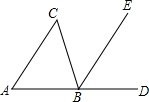 如图,点D是△ABC的边AB延长线上一点,BE∥AC,若∠C=50°,∠DBE=60°,则∠DBC的度数为( )
如图,点D是△ABC的边AB延长线上一点,BE∥AC,若∠C=50°,∠DBE=60°,则∠DBC的度数为( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
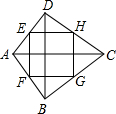 如图,四边形ABCD中,对角线AC⊥BD,且AC=BD,点E、F、G、H分别是AD、AB、BC、CD的中点.求证:四边形EFGH是正方形.
如图,四边形ABCD中,对角线AC⊥BD,且AC=BD,点E、F、G、H分别是AD、AB、BC、CD的中点.求证:四边形EFGH是正方形.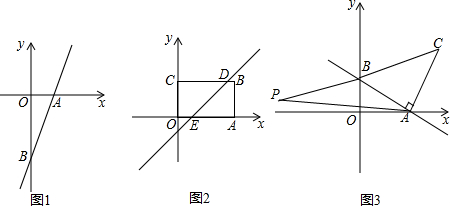
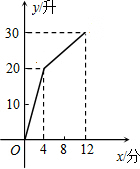 有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:分)之间的关系如图所示:
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:分)之间的关系如图所示: