题目内容
5. 已知EF⊥BC,垂足为F,∠1=∠2,AD是∠BAC的角平分线,求证:AD⊥BC.
已知EF⊥BC,垂足为F,∠1=∠2,AD是∠BAC的角平分线,求证:AD⊥BC.
分析 根据角平分线定义和已知求出∠1=∠CAD,根据平行线的性质推出AD∥EF,即可求出答案.
解答 证明:∵AD是∠BAC的角平分线,
∴∠2=∠CAD,
∵∠1=∠2,
∴∠1=∠CAD,
∴EF∥AD,
∴∠EFC=∠ADC,
∵EF⊥BC,
∴∠EFC=90°,
∴∠ADC=90°,
∴AD⊥BC.
点评 本题考查了垂直定义,平行线的性质和判定,角平分线定义的应用,能求出AD∥EF是解此题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17.已知甲、乙两人年龄之和是42,甲年龄的3倍等于乙年龄的4倍,则甲、乙两人年龄之差是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
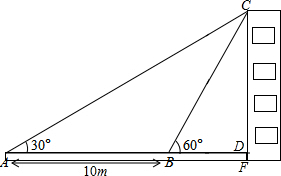 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).