题目内容
18.如图,在直角坐标系xOy中,点A、B分别在x、y轴的正半轴上,OA=3,∠ABO=30°,以A点为旋转中心,把△AOB顺时针旋转,得到△ADC,旋转角记为α(0°<α<180°).(1)求B点的坐标;
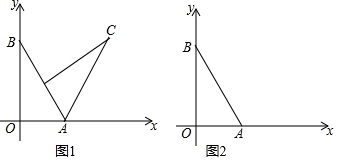
(2)当旋转后点D恰好落在AB边上时(图1),求直线CD的解析式;
(3)若旋转后满足∠AOD=∠ABO,求:α的度数以及此时直线CD的解析式.
分析 (1)利用直角三角形中,30度角所对的直角边是斜边的一半,求出AB,再用勾股定理求出OB即可;
(2)先判断出∠ADC=90°,再用含30度角的直角三角形的性质即可求出点D的坐标,即可得出结论;
(3)先求出∠BAD=60°,进而判断出点C落在x轴上,即可求出点C的坐标,再求出点D的坐标,最后用待定系数法即可得出结论.
解答 解:(1)∵点A在x轴正半轴上,且OA=3,
∴A(0,3),
在Rt△AOB中,∠ABO=30°,OA=3,
∴AB=6,OB=3$\sqrt{3}$,
∵B在y轴正半轴上,
∴B(0,3$\sqrt{3}$);
(2)如图1, 当旋转后点D恰好落在AB边上时,
当旋转后点D恰好落在AB边上时,
由旋转知,∠ADC=∠AOB=90°,AD=OA=3,
过点D作DE⊥x轴于E,
∵∠ABO=30°,
∴∠OAB=60°,
∴∠ADE=30°,
在Rt△ADE中,AE=$\frac{3}{2}$,DE=$\frac{3\sqrt{3}}{2}$,
∴OE=OA-AE=3-$\frac{3}{2}$=$\frac{3}{2}$,
∴D($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
∵A(3,0),B(0,3$\sqrt{3}$),
∴直线AB的解析式为y=-$\sqrt{3}$x+3$\sqrt{3}$,
∵CD⊥AB,
∴直线CD的解析式为y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$;
(3)如图2,
连接OD,∵∠ABO=30°,
∴∠AOD=∠ABO=30°.∠OAB=90°-30°=60°,
由旋转知,∠CAD=∠OAB=60°,OA=AD,
∴∠ODA=∠AOD=30°,
∴∠OAD=120°,
∴∠CAD=180°-120°=60°,
∴点C在x轴得正半轴上,
∵OA=3,AC=AB=6,
∴OC=OA+AC=9,
∴C(9,0),过点D作DE⊥x轴于E,
在Rt△ADE中,AD=OA=3,∠ADE=90°-∠DAE=30°,
∴AE=$\frac{3}{2}$,DE=$\frac{3\sqrt{3}}{2}$,
∴OE=OA+AE=3+$\frac{3}{2}$=$\frac{9}{2}$,
∴D($\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$),
设直线CD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{9k+b=0}\\{\frac{9}{2}k+b=\frac{3\sqrt{3}}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=3\sqrt{3}}\end{array}\right.$,
∴直线CD的解析式为y=-$\frac{\sqrt{3}}{3}$x+3$\sqrt{3}$.
点评 此题是一次函数综合题,主要考查了含30角的直角三角形的性质,旋转的性质,待定系数法,解(1)的关键是求出OB,解(2)的关键是求出点D的坐标,解(3)的关键是判断出点C落在x轴上,是一道中等难度的中考常考题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | -2 | B. | 4 | C. | -2或4 | D. | 2 |
| A. | $\frac{60}{x}$-$\frac{60}{x+1}$=3 | B. | $\frac{60}{x}$-$\frac{60}{x-1}$=3 | C. | $\frac{60}{x+1}$-$\frac{60}{x}$=3 | D. | $\frac{60}{x-1}$-$\frac{60}{x}$=3 |
 一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )
一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )| A. | 2x≥-4 | B. | 2x>-4 | C. | -2x≤-4 | D. | -2x≥4 |
| A. | $-5\frac{1}{7}$ | B. | $-3\frac{3}{7}$ | C. | $7\frac{3}{7}$ | D. | $-7\frac{3}{7}$. |
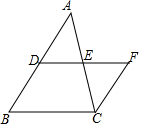 如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF.
如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF. 如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.
如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.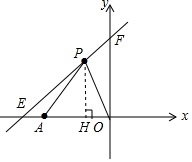 如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是第二象限内的直线l上的一个动点.
如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是第二象限内的直线l上的一个动点.