题目内容
6.已知(x2+y2)(x2+y2-2)-8=0,则x2+y2的值是( )| A. | -2 | B. | 4 | C. | -2或4 | D. | 2 |
分析 根据换元法可以求得x2+y2的值,注意x2+y2的值不小于零.
解答 解:∵(x2+y2)(x2+y2-2)-8=0,
设x2+y2=t,
∴t(t-2)-8=0,
∴t2-2t-8=0,
∴(t-4)(t+2)=0,
∴t1=4,t2=-2,
又∵x2+y2=t≥0,
∴x2+y2=t=4,
故选B.
点评 本题考查换元法解一元二次方程,解答本题的关键是明确换元法解一元二次方程的方法.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
16.已知三角形的两边之长分别为3cm和5cm,则第三边的长可能为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 10cm |
17.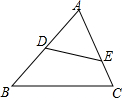 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )| A. | ∠B=∠AED | B. | AE•AC=AD•AB | C. | ∠C=∠ADE | D. | $\frac{AE}{AB}=\frac{DE}{BC}$ |
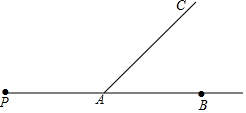 如图,P、A、B在一条直线上.
如图,P、A、B在一条直线上.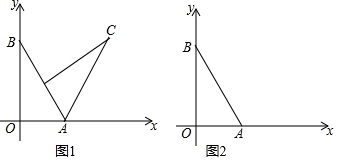
 如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为16.
如图,在周长为32的平行四边形ABCD中,AC、BD交于点O,OE⊥BD交AD于点E,则△ABE的周长为16.