题目内容
3.已知m=$\frac{1}{3}$,n=$\frac{1}{27}$,求$\frac{m-n}{\sqrt{m}-\sqrt{n}}$+$\frac{m+4n-4\sqrt{mn}}{\sqrt{m}-2\sqrt{n}}$的值.分析 首先把分式化简,合并后进一步代入数值求得答案即可.
解答 解:原式=$\sqrt{m}$+$\sqrt{n}$+$\sqrt{m}$-2$\sqrt{n}$
=2$\sqrt{m}$-$\sqrt{n}$
当m=$\frac{1}{3}$,n=$\frac{1}{27}$时,
原式=$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{9}$
=$\frac{5\sqrt{3}}{9}$.
点评 此题考查二次根式的化简求值,先化简,再进一步代入求得数值.

练习册系列答案
相关题目
8.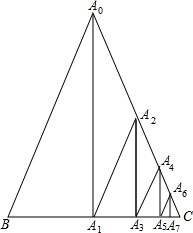 如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )
如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )
 如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )
如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )| A. | $\frac{5}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{96}$ | D. | $\frac{5}{128}$ |
 (1)如图,三角形硬纸片上标出了三个内角的编码,请用剪拼法说明三角形的内角和等于180°;
(1)如图,三角形硬纸片上标出了三个内角的编码,请用剪拼法说明三角形的内角和等于180°;