题目内容
已知如图1,抛物线 与
与 轴交于
轴交于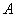 和
和 两点(点
两点(点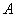 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 ,点
,点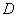 的坐标是(0,-1),连接
的坐标是(0,-1),连接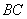 、
、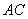 .
.
(1)求出直线 的解析式;
的解析式;
(2)如图2,若在直线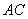 上方的抛物线上有一点
上方的抛物线上有一点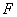 ,当
,当 的面积最大时,有一线段
的面积最大时,有一线段 (点
(点 在点
在点 的左侧)在直线
的左侧)在直线 上移动,首尾顺次连接点
上移动,首尾顺次连接点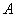 、
、 、
、 、
、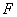 构成四边形
构成四边形 ,请求出四边形
,请求出四边形 的周长最小时点
的周长最小时点 的横坐标;
的横坐标;
(3)如图3,将 绕点
绕点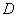 逆时针旋转
逆时针旋转 (
( ),记旋转中的
),记旋转中的 为
为 ,若直线
,若直线 与直线
与直线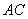 交于点
交于点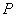 ,直线
,直线 与直线
与直线 交于点
交于点 ,当
,当 是等腰三角形时,求
是等腰三角形时,求 的值.
的值.
 | |||
 | |||

 解:(1)
解:(1) ……………………4分
……………………4分
(2)设: ,
,

=
=
=
当 时,
时, 最大
最大


作点A关于直线BD的对称点 ,把
,把 沿平行直线BD方向平移到
沿平行直线BD方向平移到 且
且 ,连接
,连接 ,交直线BD于点N,把点N沿直线BD向左平移
,交直线BD于点N,把点N沿直线BD向左平移 得点M,此时四边形AMNF的周长最小。
得点M,此时四边形AMNF的周长最小。
 ,AB=6,AK=
,AB=6,AK= ,
, ,
, ,
,

 ,
,


 ,
,








(3)当 时:
时: ;
;
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;


练习册系列答案
相关题目


 ____ _____.
____ _____.

 的开口向下,那么k的取值范围是__________.
的开口向下,那么k的取值范围是__________. ,若
,若 ,则
,则 的度数是 .
的度数是 .
