题目内容
2.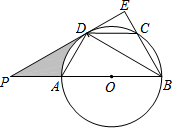 如图,四边形ABCD为⊙O的内接四边形,AB为⊙O的直径,$\widehat{AD}$=$\widehat{CD}$,过D点作DE⊥BC,交BC延长线于点E,且ED延长线交BA延长线于点P.
如图,四边形ABCD为⊙O的内接四边形,AB为⊙O的直径,$\widehat{AD}$=$\widehat{CD}$,过D点作DE⊥BC,交BC延长线于点E,且ED延长线交BA延长线于点P.(1)求证:PE为⊙O的切线;
(2)若PD=BD=2$\sqrt{3}$,求PD,PA与所围成的阴影面积(保留根号和π).
分析 (1)连结OD,如图,根据圆周角定理,由$\widehat{AD}$=$\widehat{CD}$得到∠ABD=∠CBD,加上∠OBD=∠ODB,则∠ODB=∠CBD,于是可判断OD∥BC,由于DE⊥BC,所以OD⊥DE,则可根据切线的判定定理得到PE为⊙O的切线;
(2)根据等腰三角形的性质,由DP=DB得∠P=∠PBD,则∠P=∠PBD=∠EBD,利用三角形内角和可计算出∠P=30°,则∠POD=60°,再利用∠P的正切可计算出OD=2,然后根据扇形的面积公式和S阴影部分=S△POD-S扇形AOD进行计算即可.
解答 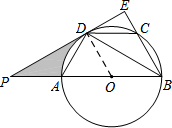 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,
∵$\widehat{AD}$=$\widehat{CD}$,
∴∠ABD=∠CBD,
而OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠CBD,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴PE为⊙O的切线;
(2)解:∵DP=DB,
∴∠P=∠PBD,
∴∠P=∠PBD=∠EBD,
而∠P+∠PBD+∠EBD=90°,
∴∠P=30°,
∵OD⊥PD,
∴∠POD=60°,
∵tan∠P=$\frac{OD}{PD}$,
∴OD=2$\sqrt{3}$tan30°=2,
∴S阴影部分=S△POD-S扇形AOD
=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60•π•{2}^{2}}{360}$
=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积的计算.

练习册系列答案
相关题目
11. 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
如图是由4个大小相等的正方形搭成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
12.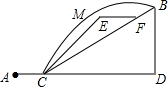 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )| A. | A→C→D→B | B. | A→C→F→B | C. | A→C→E→F→B | D. | A→C→M→B |
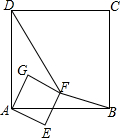 正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.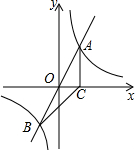 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.