题目内容
12.函数y=ax2+bx+c的三项系数分别为a、b、c,则定义[a,b,c]为该函数的“特征数”.如:函数y=x2+3x-2的“特征数”是[1,3,-2],函数y=-x+4的“特征数”是[0,-1,4].如果将“特征数”是[2,0,4]的函数图象向左平移3个单位,得到一个新的函数图象,那么这个新图象相应的函数表达式是y=2(x+3)2+4.分析 先写出抛物线的解析式,然后求出顶点坐标,再根据向左平移横坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出函数表达式即可.
解答 解:∵“特征数”是[2,0,4],
∴函数解析式为y=2x2+4,
∴函数的顶点坐标为(0,4),
∵函数图象向左平移3个单位,
∴得到的新的函数图象的顶点坐标为(3,4),
∴函数表达式为y=2(x+3)2+4.
故答案为:y=2(x+3)2+4.
点评 本题考查了二次函数图象与几何变换,读懂题目信息理解函数的“特征数”是解题的关键,此类题目,利用顶点的变化确定函数解析式的更简便.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
17. 如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是( )
如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是( )
 如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是( )
如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
4.一个不透明的口袋中,装有5个红球,2个黄球,1个白球,这些球除颜色外其余都相同,从口袋中随机摸一个球,则摸到红球的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |

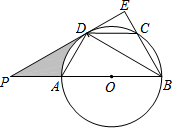 如图,四边形ABCD为⊙O的内接四边形,AB为⊙O的直径,$\widehat{AD}$=$\widehat{CD}$,过D点作DE⊥BC,交BC延长线于点E,且ED延长线交BA延长线于点P.
如图,四边形ABCD为⊙O的内接四边形,AB为⊙O的直径,$\widehat{AD}$=$\widehat{CD}$,过D点作DE⊥BC,交BC延长线于点E,且ED延长线交BA延长线于点P.