题目内容
3. 如图,在平面直角坐标系中,长方形ABCD的边BC在x轴上.如果点A坐标是(-1,4$\sqrt{2}$),C点坐标是(3,0).
如图,在平面直角坐标系中,长方形ABCD的边BC在x轴上.如果点A坐标是(-1,4$\sqrt{2}$),C点坐标是(3,0).(1)求B点和D点的坐标;
(2)将这个长方形向下平移2个单位长度,四个顶点的坐标变为多少?请你写出平移后四个顶点的坐标;
(3)如果Q点以每秒$\sqrt{2}$个单位长度的速度在长方形ABCD的边上从A出发到C点停止,沿着A→D→C的路径运动,那么当Q点的运动时间分别是1秒和4秒时,△BCQ的面积各是多少?请你分别求出来.
分析 (1)根据平行于坐标轴的点的坐标特点即可求得答案;
(2)根据平移与坐标变化的关系即可求得答案;
(3)根据运动时间求得三角形的高,然后根据公式计算即可.
解答 解:(1)根据题意可知,点B的坐标是(-1,0),点D的坐标是(3,$4\sqrt{2}$).
(2)按要求平移长方形后四个顶点的坐标分别是(-1,4$\sqrt{2}$-2)、(-1,-2)、(3,-2)、(3,4$\sqrt{2}$-2).
(3)运动时间1秒时,△BCQ的面积=$\frac{1}{2}×4×4\sqrt{2}$=$8\sqrt{2}$,
运动时间4秒时,△BCQ的面积=$\frac{1}{2}×4×({4+4\sqrt{2}-4\sqrt{2}})=8$.
点评 本题主要考查的是坐标与图形的变化,掌握平行于坐标轴的点的坐标特点和平移与坐标变化的规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.化简:$\frac{\sqrt{2{5}^{2}-{7}^{2}}}{\sqrt{27}}$的结果是( )
| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{8\sqrt{3}}{9}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
8.下列调查所选取的样本中,具有代表性的是( )
| A. | 了解全校同学喜欢课程的情况,对某班男同学进行调查 | |
| B. | 了解某小区居民防火意识,对你们班同学进行调查 | |
| C. | 了解某商场的平均日营业额,选在周末进行调查 | |
| D. | 了解全校同学对动画电视节目的喜爱情况,上学时在学校门口随意调查100名同学 |
 如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.
如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.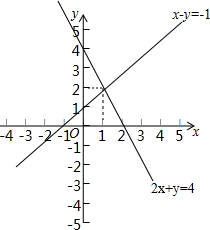 如图,在同一个平面直角坐标系中,画出二元一次方程组$\left\{{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}}\right.$中的两个二元一次方程的图象,由这两个二元一次方程的图象,可得出这个二元一次方程组的解是$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$.
如图,在同一个平面直角坐标系中,画出二元一次方程组$\left\{{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}}\right.$中的两个二元一次方程的图象,由这两个二元一次方程的图象,可得出这个二元一次方程组的解是$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$.