题目内容
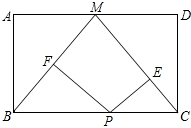 如图,在矩形ABCD中,M是AD的中点,连接BM、CM,点P是BC边上的动点,作PE⊥MC于E点,PF⊥MB于F点,当矩形的长与宽是什么关系时,四边形PEMF是矩形?并证明.
如图,在矩形ABCD中,M是AD的中点,连接BM、CM,点P是BC边上的动点,作PE⊥MC于E点,PF⊥MB于F点,当矩形的长与宽是什么关系时,四边形PEMF是矩形?并证明.考点:矩形的判定与性质
专题:
分析:当长=宽的2倍的时候,根据4个角为直角即可证明四边形PEMF是矩形.
解答:解:∵M是AD的中点,AD=2AB
∴AM=MD=AB=CD,
∵矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=180°-45°-45°=90°,
∴∠EPF=360°-90°-90°-90°=90°
∴四边形PEMF是矩形.
∴AM=MD=AB=CD,
∵矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=180°-45°-45°=90°,
∴∠EPF=360°-90°-90°-90°=90°
∴四边形PEMF是矩形.
点评:本题考查了矩形各内角为90°的性质,考查了矩形的判定,本题求证∠BMC=90°是解题的关键.

练习册系列答案
相关题目
 如图,将△ABC(其中∠BAC=50°)绕点A逆时针方向旋转一个锐角到△ADE的位置,这时恰好有AE⊥AB,则下列说法正确的是( )
如图,将△ABC(其中∠BAC=50°)绕点A逆时针方向旋转一个锐角到△ADE的位置,这时恰好有AE⊥AB,则下列说法正确的是( )| A、旋转角为40° |
| B、旋转角为45° |
| C、旋转角为50° |
| D、旋转角为90° |
一条弧所对的圆心角是90°,半径为1,则这条弧的长度是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,正三角形ABC的三边表示三面镜子,AP=
如图,正三角形ABC的三边表示三面镜子,AP=| 1 |
| 3 |
| A、3n | B、6n | C、8n | D、9n |
下列各数中,最小的数是( )
| A、-2 | B、-1 | C、0 | D、-π |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0.其中正确的结论有
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0.其中正确的结论有