题目内容
 如图,正三角形ABC的三边表示三面镜子,AP=
如图,正三角形ABC的三边表示三面镜子,AP=| 1 |
| 3 |
| A、3n | B、6n | C、8n | D、9n |
考点:等边三角形的性质,轴对称的性质
专题:规律型
分析:根据等边三角形的性质可知当光线第一次回到点P时,这束光经过了三圈反射,其路线为1+2+1+2+1+2=9,而当第n次经过P点时,则其经过的路线总长为9n.
解答: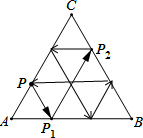 解:∵△ABC为等边三角形,
解:∵△ABC为等边三角形,
∴∠A=60°,
∵AP=
AC=1,且∠APP1=60°,
∴△APP1为等边三角形,
∴AP=PP1,P1P2=PC,
∴一次反射路线长为3,
如图可知当第一次光线回到P点时,这束光经过了三圈反射,其路线为1+2+1+2+1+2=9,
而当第n次经过P点时,则其经过的路线总长为9n.
故选D.
 解:∵△ABC为等边三角形,
解:∵△ABC为等边三角形,∴∠A=60°,
∵AP=
| 1 |
| 3 |
∴△APP1为等边三角形,
∴AP=PP1,P1P2=PC,
∴一次反射路线长为3,
如图可知当第一次光线回到P点时,这束光经过了三圈反射,其路线为1+2+1+2+1+2=9,
而当第n次经过P点时,则其经过的路线总长为9n.
故选D.
点评:本题主要考查等边三角形的性质,解题的关键是分析光线第一次回到点P时经过了几圈反射.

练习册系列答案
相关题目
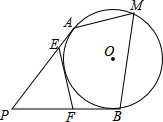 如图,PA,PB分别切⊙O于A、B,圆周角∠AMB=60°,EF切⊙O于C,交PA,PB于E,F,△PEF的外心在PE上,PA=3,则AE的长为( )
如图,PA,PB分别切⊙O于A、B,圆周角∠AMB=60°,EF切⊙O于C,交PA,PB于E,F,△PEF的外心在PE上,PA=3,则AE的长为( )A、3-
| ||
B、4-2
| ||
| C、1 | ||
D、2
|
下列各式变形正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,已知在△ABC中,AB=AC,∠B=70°,BD=CF,BE=DC.
如图,已知在△ABC中,AB=AC,∠B=70°,BD=CF,BE=DC.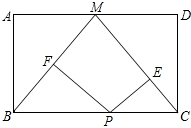 如图,在矩形ABCD中,M是AD的中点,连接BM、CM,点P是BC边上的动点,作PE⊥MC于E点,PF⊥MB于F点,当矩形的长与宽是什么关系时,四边形PEMF是矩形?并证明.
如图,在矩形ABCD中,M是AD的中点,连接BM、CM,点P是BC边上的动点,作PE⊥MC于E点,PF⊥MB于F点,当矩形的长与宽是什么关系时,四边形PEMF是矩形?并证明.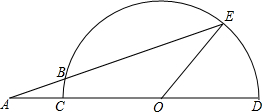 如图,已知CD是半圆的直径,O是圆心,E是半圆上一点,且∠EOD=45°,A是DC延长线上的一点,AE交半圆于点B,AB=OC=2,求弓形BE的高.
如图,已知CD是半圆的直径,O是圆心,E是半圆上一点,且∠EOD=45°,A是DC延长线上的一点,AE交半圆于点B,AB=OC=2,求弓形BE的高.