若不等式组$\left\{\begin{array}{l}{5x+2≤3x-5}\\{-x+5＜a}\end{array}\right.$无解.则a的取值范围是( )A．a$≤\frac{17}{2}$B．a≤12C．a＜$\frac{17}{2}$D．a＜12 题目和参考答案——青夏教育精英家教网—

题目内容

8．若不等式组$\left\{\begin{array}{l}{5x+2≤3x-5}\\{-x+5＜a}\end{array}\right.$无解，则a的取值范围是（　　）

A．

a$≤\frac{17}{2}$

B．

a≤12

C．

a＜$\frac{17}{2}$

D．

a＜12

分析不等式组中两不等式整理求出解集，根据不等式组无解，确定出a的范围即可．

解答解：不等式组整理得：$\left\{\begin{array}{l}{x≤-\frac{7}{2}}\\{x＞5-a}\end{array}\right.$，
由不等式组无解，得到5-a≥-$\frac{7}{2}$，即10-2a≥-7，
解得：a≤$\frac{17}{2}$，
故选：A．

点评此题考查了不等式的解集，熟练掌握不等式取解集的方法是解本题的关键．

练习册系列答案

19．某数学兴趣小组开展了一次活动，过程如下：
如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小勇将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．
（1）如图1，小勇在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠MAB，则AE也平分∠MAC．请你证明小勇发现的结论；
（2）小勇在旋转的过程中得到图2所示的图形时，发现线段BD、CE、DE这三条线段可以围成以DE为斜边的直角三角形，请你证明这个结论；
（3）小亮重新从AB边开始绕点A逆时针旋转三角板，并探究：当135°＜α＜180°时（如图3），形成的线段BD、CE、DE是否仍能围成以DE为斜边的直角三角形？若能，给出证明；若不能，说明理由．

16．在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出下列定义：若b′=$\left\{\begin{array}{l}{b，}&{a≥1}\\{-b，}&{a＜1}\end{array}\right.$，则称点Q为点的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5），如果一个点的限变点的坐标是（$\sqrt{3}$，-1），那么这个点的坐标是（　　）

3．下列四个图形中，是中心对称而不是轴对称的是（　　）

13．

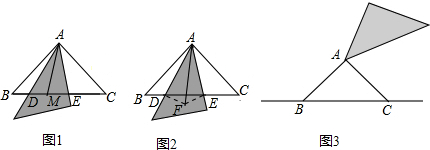
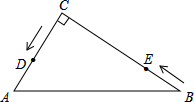如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s的速度沿折线C→A→B向点B运动，同时，点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为ts（0＜t＜8）．
（1）AB=10cm，sinB=$\frac{3}{5}$；
（2）当△BDE是直角三角形时，求t的值；
（3）若四边形CDEF是以CD、DE为一组邻边的平行四边形，
①设?CDEF的面积为Scm²，求S于t的函数关系式；
②是否存在某个时刻t，使?CDEF为菱形？若存在，求出t的值；若不存在，请说明理由．

20．如果a^2n-1•aⁿ⁺²=a⁷，则n的值是（　　）

17．计算（写出计算过程）：
（1）2$\sqrt{6}$+（$\sqrt{2}$）⁰-$\sqrt{6}$；
（2）$\sqrt{5}$×$\sqrt{13}$$÷\frac{1}{2\sqrt{5}}$．

18．若a＞b，则下列式子中错误的是（　　）

$\frac{a}{5}$＞$\frac{b}{5}$

试题分类