Question

如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，点D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立.

    

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由.

(2)当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G.

①求证：BD⊥CF；

②当AB=4，AD=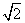时，求线段BG的长.

Answer 1

(1)BD=CF成立.

理由：∵△ABC是等腰直角三角形，四边形ADEF是正方形，

∴AB=AC，AD=AF，∠BAC=∠DAF=90°.

∵∠BAD=∠BAC-∠DAC，

∠CAF=∠DAF-∠DAC，

∴∠BAD=∠CAF，

∴△BAD≌△CAF(SAS).

∴BD=CF.

(2)①证明：设BG交AC于点M.

∵△BAD≌△CAF(已证)，∴∠ABM=∠GCM.

∵∠BMA=∠CMG，∴△BMA∽△CMG.

∴∠BGC=∠BAC=90°.∴BD⊥CF.

②过点F作FN⊥AC于点N.

∵在正方形ADEF中，AD=，

∴AN=FN=AE=1.

∵在等腰直角△ABC中，AB=4，

∴CN=AC-AN=3，BC==4.

∴在Rt△FCN中，tan∠FCN==.

∴在Rt△ABM中，

tan∠ABM==tan∠FCN=.

∴AM=×AB=.

∴CM=AC-AM=4-=，

BM==.

∵△BMA∽△CMG，∴ =.

∴=.∴CG=.

∴在Rt△BGC中，BG==.