题目内容
如图，△ABO与△CDO关于点O中心对称，点E，F在线段AC上，且AF=CE.求证：FD=BE.
.证明：∵△ABO与△CDO关于O点中心对称，
∴△ABO≌△CDO.∴AO=CO，BO=DO.
又∵AF=CE，∴AO-AF=CO-CE，即OF=OE.
∵∠FOD=∠EOB，∴△FOD≌△EOB(SAS).
∴FD=BE.
练习册系列答案
相关题目
某次射击训练中，一小组的成绩如下表所示：已知该小组的平均成绩为8环，那么成绩为9环的人数是3.
| 环数 | 7 | 8 | 9 |
| 人数 | 3 | 4 |
轴对称与轴对称图形
| 轴对称 | 轴对称图形 | |
| 定义 | 把一个图形沿某一条直线折叠，如果能够与另一个图形⑥ ，那么就说这两个图形成轴对称，这条直线就是⑦ ，两个图形的对应点叫做对称点. | 如果一个图形沿某条直线对折，对折的两部分能够完全⑧ ，那么就称这样的图形为轴对称图形，这条直线叫做这个图形的⑨ . |
| 区别 | 轴对称是指两个全等图形之间的相互位置关系. | 轴对称图形是指具有特殊形状的一个图形. |
| 轴对称的性质 | 1.对称点的连线被对称轴⑩ ； 2.对应线段⑪ ； 3.对应线段或延长线段的交点在⑫ 上； 4.成轴对称的两个图形⑬ . |
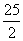π B.13π C.25π D.25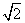
，B，C，D的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是( )
( )