题目内容
2．
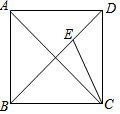如图，正方形ABCD中，E是BD上一点，BE=BC，则∠BEC的度数是（ ）| A． | 45° | B． | 60° | C． | 67.5° | D． | 82.5° |
分析 利用正方形的性质，可知∠CBE=45°，再根据等腰三角形的性质即可解决问题．
解答 解：∵四边形ABCD是正方形，
∴∠CBD=45°，
∵BC=BE，
∴∠BEC=∠BCE=$\frac{1}{2}$（180°-45°）=67.5°，
故选C．
点评 本题考查正方形的性质．等腰三角形的性质等知识，熟练掌握正方形的性质是解决问题的关键．
练习册系列答案
相关题目
13．下列说法正确的是（ ）
| A． | 不可能事件发生的概率为0 | |
| B． | 随机事件发生的概率为$\frac{1}{2}$ | |
| C． | 概率很小的事件不可能发生 | |
| D． | 投掷一枚质地均匀的硬币1000次，正面朝上的次数一定是500次 |
17．
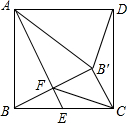如图，在正方形ABCD中，点E是 BC边的中点，点B′与点B关于AE对称，BB′与AE交
于点F．下列结论错误的是（ ）
如图，在正方形ABCD中，点E是 BC边的中点，点B′与点B关于AE对称，BB′与AE交于点F．下列结论错误的是（ ）
| A． | AB′=AD | B． | ∠ADB′=75° | ||
| C． | ∠CB′D=135° | D． | △FCB′是等腰直角三角形 |
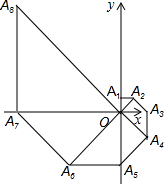如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1=A1A2=1，以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4，…，依此规律，得到等腰直角三角形OA2017A2018，则点A2017的坐标为（0，（$\sqrt{2}$）2016）或（0，21008）．
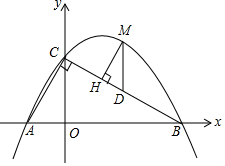如图，直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点，点A在x轴上，∠ACB=90°，抛物线y=ax2+bx+$\sqrt{3}$经过A，B两点．