题目内容
因式分解:
(1)x3-3x2+4
(2)x3-11x2+31x-21.
(1)x3-3x2+4
(2)x3-11x2+31x-21.
考点:因式分解
专题:
分析:(1)先分组为(x3-2x2)+(-x2+4),再用平方差公式和提公因式因式分解;
(2)首先利用拆项法将原式变形,进而再提取公因式,结合十字相乘法分解因式得出即可.
(2)首先利用拆项法将原式变形,进而再提取公因式,结合十字相乘法分解因式得出即可.
解答:解:(1)x3-3x2+4
=x3-2x2-x2+4
=x2(x-2)+(x+2)(2-x)
=(x-2)(x2-x+2)
=(x-2)(x-2)(x+1)
=(x-2)2(x+1);
(2)x3-11x2+31x-21
=(x3-x2)-(10x2-10x)+(21x-21)
=x2(x-1)-10x(x-1)+21(x-1)
=(x2-10x+21)(x-1)
=(x-3)(x-7)(x-1)
=(x-1)(x-3)(x-7).
=x3-2x2-x2+4
=x2(x-2)+(x+2)(2-x)
=(x-2)(x2-x+2)
=(x-2)(x-2)(x+1)
=(x-2)2(x+1);
(2)x3-11x2+31x-21
=(x3-x2)-(10x2-10x)+(21x-21)
=x2(x-1)-10x(x-1)+21(x-1)
=(x2-10x+21)(x-1)
=(x-3)(x-7)(x-1)
=(x-1)(x-3)(x-7).
点评:此题主要考查了因式分解法的应用,利用分组分解法正确分解因式是解题关键.

练习册系列答案
相关题目
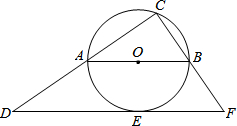 如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )
如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )A、
| ||
B、
| ||
C、
| ||
D、
|