Question

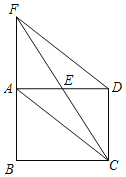
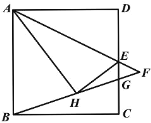
【题目】如图，在正方形ABCD中，AB＝2，点E是CD的中点，连接AE，将△ADE沿AE折叠至△AHE，连接BH，延长AE，BH交于点F；BF，CD交于点G，则FG=_______．

Answer 1

【答案】

【解析】

过点H作MN∥AD，交AB于M，交CD于N，通过证明△AMH∽△HNE，可得，进而得出MH＝2EN，HN＝，可求NE的长，即可求BM，MH，HN的长，由平行线分线段成比例可得HG，GN，EG的长，再次利用平行线分线段成比例可得FG的长．

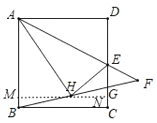
解：过点H作MN∥AD，交AB于M，交CD于N，

∴∠BAD＝∠BMN＝90°，∠D＝∠MNC＝90°，

∴四边形ADNM是矩形，

∴AM＝DN，MN＝AD＝2，

∵将△ADE沿AE折叠至△AHE，

∴AH＝AD＝2，∠AHE＝90°，HE＝DE＝1，

∴∠AHM＋∠EHN＝90°，且∠MAH＋∠AHM＝90°，

∴∠MAH＝∠EHN，且∠AMH＝∠ENH＝90°，

∴△AMH∽△HNE，

∴，

∴，

∴MH＝2NE，HN＝，

∵MH＋HN＝MN＝2，

∴2NE＋＝2，

∴NE＝，

∴MH＝，HN＝，AM＝，

∴BM＝，

∴BH＝，

∵AB∥CD，

∴，

∴NG＝，HG＝，

∴BG＝，EG＝，

∵AB∥CD，

∴，即

∴FG＝，

故答案为：．