题目内容
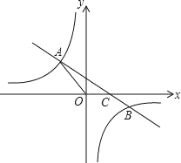
【题目】如图， 
为坐标原点，点
在
轴的正半轴上，四边形
是平行四边形， 
，反比例函数
在第一象限内的图像经过点
，与
交于点
，若点为的中点，且
的面积为12，则
的值为（ ）
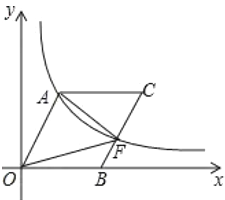
A.16B.24C.36D.48
【答案】A
【解析】
过点A作AM⊥OB于M，FN⊥OB于N，，设OA=5k，通过解直角三角形得出AM=4k,OM=3k,m=12k2,，再根据S四边形OAFN=S梯形AMNF+S△AOM=S△AOF+S△OFN得到S梯形AMNF=S△AOF=12，得出
(4k+2k)3k=12，得到k2的值，再求m得值即可．
解：过点A作AM⊥OB于M，FN⊥OB于N，
设OA=5k，
∵
∴AM=4k,OM=3k,m=12k2,
∵四边形OACB是平行四边形，
为
的中点，
∴FN=2k，ON=6k，
∵S△AOM=S△OFN，
S四边形OAFN=S梯形AMNF+S△AOM=S△AOF+S△OFN，
∴S梯形AMNF=S△AOF=12，
∴ (4k+2k)3k=12，
∴k2=
，
∴m=12k2=16.
故选A.
练习册系列答案
相关题目
