Question

【题目】已知双曲线与在第一象限内交于两点，，则扇形的面积是__________．

Answer 1

【答案】

【解析】

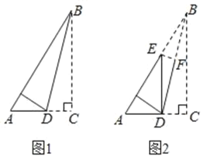
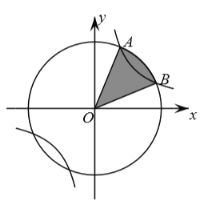
设⊙O的半径OA=OB=r，连接AB，作直线y=x，与AB交于点C，过A作AD⊥y轴于点D，过B作BE⊥x轴于点E，过A作AF⊥OB于点F．由圆与双曲线的对称性得△AOD≌△AOC≌△BOC≌△BOE，进而由反比例函数的比例系数的几何意义得△AOB的面积，再由三角形的面积公式求得圆的半径，最后由扇形的面积公式求得结果．

设⊙O的半径OA=OB=r，连接AB，作直线y=x，与AB交于点C，过A作AD⊥y轴于点D，过B作BE⊥x轴于点E，过A作AF⊥OB于点F．

∵⊙O在第一象限关于y=x对称，也关于y=x对称，
∴∠AOC=∠BOC，OC⊥AB，∠AOD=∠BOE，
∵∠AOB=45°，
∴∠AOD=∠AOC=∠BOC=∠BOE=22.5°，
由对称性知，△AOD≌△AOC≌△BOC≌△BOE，
由反比例函数的几何意义知，S△AOD＝S△BOE＝×4＝2，
∴S△AOC=S△BOC=2，
∴S△AOB=2+2=4，
∵∠AOB=45°，

∴OA=AF=OF
∴AF=OF=OA＝r，
∵S△AOB=OBAF，
∴4=r×r，
∴r2＝8，
∴S扇形OAB＝＝

故答案为：．