题目内容

求第n行各数之和.
考点:规律型:数字的变化类
专题:
分析:数为自然数,每行数的个数为1,3,5,…的奇数列;第n行最后一数为n2,则第一个数为n2-2n+2,每行数由题意知每行数的个数为1,3,5,…的奇数列,故个数为2n-1;从而列式求得答案.
解答:解:第n行最后一数为n2,则第一个数为n2-2n+2,每行数由题意知每行数的个数为1,3,5,…的奇数列,故个数为2n-1;
第n行各数之和:
×(2n-1)=(n2-n+1)(2n-1).
第n行各数之和:
| n2-2n+2+n2 |
| 2 |
点评:此题考查数字的变化规律,找出数字之间的联系,利用计算规律解决问题.

练习册系列答案
相关题目
 如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )
如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )| A、4条棱 | B、5条棱 |
| C、6条棱 | D、7条棱 |
下列命题中的假命题是( )
| A、圆心角的度数与它所对的弧的度数相等 |
| B、等弧所对的弦相等 |
| C、90°的圆周角所对的弦是直径 |
| D、三点确定一个圆 |
 如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A、AM=CN |
| B、AM∥CN |
| C、AB=CD |
| D、∠M=∠N |
小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
| A、测量三边对应相等 |
| B、测量两角及其夹边对应相等 |
| C、测量两边及除夹角外的另一角对应相等 |
| D、测量两边及其夹角对应相等 |
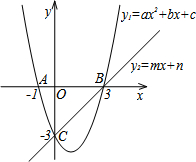 如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知:
如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知: 如图,OA=OC,请你添加一个条件:
如图,OA=OC,请你添加一个条件: