题目内容
16.王翔同学在一次跳高训练中采用了背跃式,跳跃路线正好和抛物线y=-2x2+3x+3相吻合,那么他能跳过的最大高度为$\frac{33}{8}$m.分析 根据二次函数解析式及顶点坐标公式,求顶点纵坐标,即函数最大值即可.
解答 解:根据顶点坐标公式,
抛物线y=-2x2+3x+3的顶点纵坐标是y=$\frac{-4×2×3-{3}^{2}}{-4×2}$=$\frac{33}{8}$,
即他能跳过的最大高度为:$\frac{33}{8}$m,
故答案为:$\frac{33}{8}$.
点评 本题考查的是二次函数在实际生活中的应用,熟记二次函数解析式的顶点坐标公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一种树苗,每年高度与树主干直径变化数据如下:
如果以后每年的生长都符合这一规律.
(1)当树干直径是9.8cm时,树的高度是多少?
(2)树干直径是多少时,树高450cm?
| 直径(cm) | 2 | 4 | 6 | 8 | 10 |
| 高度(cm) | 100 | 150 | 200 | 250 | 300 |
(1)当树干直径是9.8cm时,树的高度是多少?
(2)树干直径是多少时,树高450cm?
5.下列运算正确的是( )
| A. | (a2)3=a5 | B. | (a-b)2=a2-b2 | C. | 2a2+a=3a3 | D. | (-a)3•a2=-a5 |

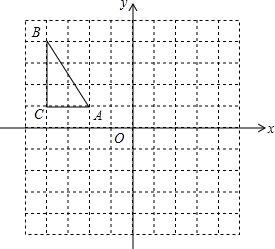 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空: