题目内容
1.一种树苗,每年高度与树主干直径变化数据如下:| 直径(cm) | 2 | 4 | 6 | 8 | 10 |
| 高度(cm) | 100 | 150 | 200 | 250 | 300 |
(1)当树干直径是9.8cm时,树的高度是多少?
(2)树干直径是多少时,树高450cm?
分析 由数据可知:设每年高度ycm,树主干直径xcm,每年高度与树主干直径符合一次函数,设出一次函数解析式,利用待定系数法求函数解析式.
(1)把x=9.8代入函数解析式得出答案即可;
(2)把y=450代入函数解析式得出答案即可.
解答 解:由数据可知:设每年高度ycm,树主干直径xcm,每年高度与树主干直径的关系式为y=kx+b,
代入(2,100),(4,150)得$\left\{\begin{array}{l}{2k+b=100}\\{4k+b=150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=25}\\{b=50}\end{array}\right.$.
因此每年高度与树主干直径的关系式为y=25x+50.
(1)当x=9.8时,
y=25×9.8+50=295.
答:树的高度是295cm;
(2)当y=450时,
25x+50=450,
解得:x=16.
答:树干直径是16cm时,树高450cm.
点评 此题考查一次函数的实际运用,掌握待定系数法求函数解析式的方法与步骤是解决问题的关键.

练习册系列答案
相关题目
11.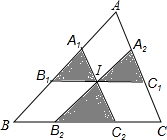 如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
 如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )| A. | 12 | B. | 15 | C. | 18 | D. | 20 |
12.点P(5,-1)关于原点的对称点P′的坐标为( )
| A. | (5,1) | B. | (-5,-1) | C. | (-5,1) | D. | (-1,5) |
10.下列运算结果为负数的是( )
| A. | (-2013)-1 | B. | (-1)2012 | C. | (-1)×(-2012) | D. | -1-(-2013) |

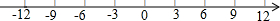 如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动.3秒后,两点相距12个单位长度.已知动点A、B的速度比是1:3(速度单位:1个单位长度/秒).
如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动.3秒后,两点相距12个单位长度.已知动点A、B的速度比是1:3(速度单位:1个单位长度/秒).