题目内容
已知一元二次方程mx2+nx+(n-m)=0(m≠0),则判别式△= ,该方程根的情况是 .
考点:根的判别式,一元二次方程的定义
专题:
分析:根据方程的系数可以直接求出其判别式的值,然后根据求出的判别式即可判断方程的根的情况.
解答:解:∵a=m,b=n,c=n-m,
∴△=n2-4m(n-m)=n2-4mn+4m2=(n-2m)2≥0,
∴方程有两个实数根.
故答案为:(n-2m)2,有两个实数根.
∴△=n2-4m(n-m)=n2-4mn+4m2=(n-2m)2≥0,
∴方程有两个实数根.
故答案为:(n-2m)2,有两个实数根.
点评:本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
已知在Rt△ABC中,∠ACB=Rt∠,AC=5,BC=12,则Rt△ABC的外接圆的半径为( )
| A、12 | ||
B、
| ||
| C、6 | ||
D、
|
计算(-3)0的结果是( )
| A、-1 | B、1 | C、0 | D、-3 |
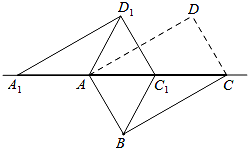 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1. 已知AC=6,∠ACB=30°,若要使四边形ABC1D1是菱形,则平移的距离等于
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1. 已知AC=6,∠ACB=30°,若要使四边形ABC1D1是菱形,则平移的距离等于