题目内容
12.下列命题:①方程x2=x的解是x=1;
②$\sqrt{4}$的算术平方根是$\sqrt{2}$;
③有两边和一角相等的两个三角形全等;
④连接任意四边形各边中点的四边形是平行四边形,
其中真命题有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 通过解一元二次方程可对①进行判断;根据算术平方根的定义对②进行判断;根据全等三角形的判定方法对③进行判断;根据三角形中位线的性质和平行四边形的判定方法对④进行判断.
解答 解:方程x2=x的解是x=1或x=0,所以①错误;
$\sqrt{4}$的算术平方根是$\sqrt{2}$,所以②正确;
有两边和它们的夹角相等的两个三角形全等,所以③错误;
连接任意四边形各边中点的四边形是平行四边形,所以④正确.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.绝对值是10的有理数是( )
| A. | 10 | B. | -10 | C. | ±10 | D. | 以上都对 |
3.一个正多边形的中心角等于30°,那么这个正多边形的边数为( )
| A. | 3 | B. | 6 | C. | 8 | D. | 12 |
7.下列实数中,是无理数的是( )
| A. | $\sqrt{4}$ | B. | cos60° | C. | π-3.14 | D. | $\frac{22}{7}$ |
17.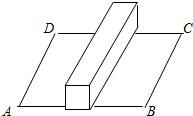 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
1.从长度分别为2、3、4、5的4条线段中任取3条,能构成钝角三角形的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.
矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.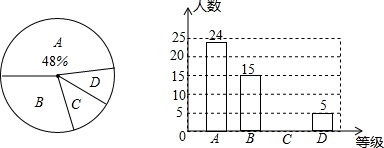
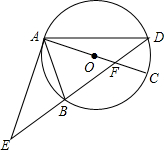 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.