Question

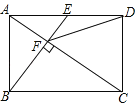
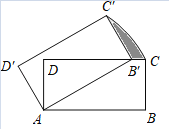
【题目】如图，矩形ABCD中，AB＝，BC＝1，将矩形ABCD绕点A旋转得到矩形AB′C′D′，点C的运动路径为弧CC′，当点B′落在CD上时，则图中阴影部分的面积为______

Answer 1

【答案】﹣+

【解析】

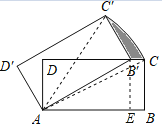
如图连接AC，AC′，过B′作B′E⊥AB于E，于是得到B′E＝BC＝1，根据旋转的性质得到AB′＝AB＝，AC′＝AC＝，B′C＝BE＝﹣1，根据勾股定理得到AE＝1，求得∠B′AB＝∠C′AC＝45°，根据扇形和三角形的面积公式即可得到结论．

解：如图连接AC，AC′，过B′作B′E⊥AB于E，

则B′E＝BC＝1，

∵将矩形ABCD绕点A旋转得到矩形AB′C′D′，

∴AB′＝AB＝，AC′＝AC＝，B′C＝BE＝﹣1，

∴AE＝＝1，

∴∠B′AB＝∠C′AC＝45°，

∴图中阴影部分的面积＝S扇形C′AC﹣S△ABC′﹣S△AB′C＝﹣﹣×(﹣1)×1＝﹣+，

故答案为：﹣+．