题目内容
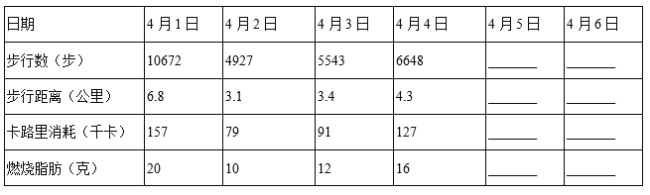
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() .
.
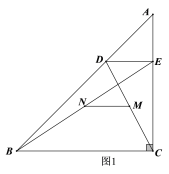

(1)问题发现
图1中,线段![]() 与线段
与线段![]() 之间的数量关系为_____________;
之间的数量关系为_____________;
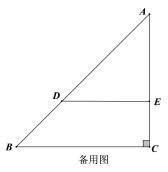
(2)类比探究
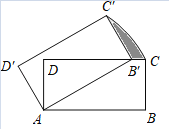
将![]() 绕点
绕点![]() 顺时针旋转到图2的位置,连接
顺时针旋转到图2的位置,连接![]() ,
,![]() .试问(1)中的结论是否仍然成立?请判断并说明理由;
.试问(1)中的结论是否仍然成立?请判断并说明理由;
(3)问题解决
若![]() ,将
,将![]() 绕点
绕点![]() 在平面内顺时针旋转,请直接写出线段
在平面内顺时针旋转,请直接写出线段![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)结论成立,证明详见解析;(3)
;(2)结论成立,证明详见解析;(3)![]() 的最大值为4.
的最大值为4.
【解析】
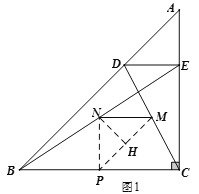
(1)如图1,取![]() 的中点P,连接
的中点P,连接![]() ,
,![]() ,先根据三角形中位线定理得
,先根据三角形中位线定理得![]() ,
,![]() ,
,![]() ,进一步即得
,进一步即得![]() ,再证明
,再证明![]() 为等腰直角三角形,即可得到
为等腰直角三角形,即可得到![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)类似(1)的证法,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,如图2,先根据两边成比例且夹角相等证明
,如图2,先根据两边成比例且夹角相等证明![]() ∽
∽![]() ,从而得出
,从而得出![]() ,
,![]() ;再结合三角形中位线定理和平行线的性质得出∠NPM=45°,
;再结合三角形中位线定理和平行线的性质得出∠NPM=45°,![]() ,进而可得
,进而可得![]() 为等腰直角三角形,问题即得解决;
为等腰直角三角形,问题即得解决;
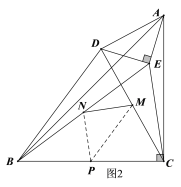
(3)如图3,由题意可知点![]() 在以
在以![]() 为圆心、
为圆心、![]() 为半径的圆上运动,显然当C、A、E三点共线且C、E在点A的两侧时CE最大,求出CE的最大值后,由(2)的结论即得MN的最大值.
为半径的圆上运动,显然当C、A、E三点共线且C、E在点A的两侧时CE最大,求出CE的最大值后,由(2)的结论即得MN的最大值.
解:(1)关系为:![]() .
.
证明:如图1,设点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴由三角形中位线定理可得![]() ,
,![]() ,
,
且![]() .
.
由已知可得![]() ,所以
,所以![]() .
.
过点![]() 作
作![]() 于点
于点![]() .
.
则△PNH是等腰直角三角形,∴HP=HN=![]() PN,
PN,
又∵![]() ,
,
∴![]() .
.
所以![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
所以![]() .
.
(2)结论仍然成立.
理由如下:如图2,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ∽
∽![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中位线,
的中位线,
∴![]() ,
,![]() 且
且![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]()
=![]() ,且
,且![]() .
.
由(1)的证明知![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]() . ∴
. ∴![]() .
.
(3)![]() 的最大值为4.
的最大值为4.
如图3,点![]() 在以
在以![]() 为圆心、
为圆心、![]() 为半径的圆上运动,当C、A、E三点共线且C、E在点A的两侧时CE最大,∵
为半径的圆上运动,当C、A、E三点共线且C、E在点A的两侧时CE最大,∵![]() ,∴AE=3,所以
,∴AE=3,所以![]() 的最大值=5+3=8.
的最大值=5+3=8.
所以![]() 的最大值为4.
的最大值为4.

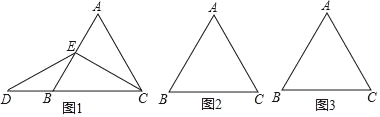
【题目】某“兴趣小组”根据学习函数的经验,对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.

(1)函数y=x+![]() 的自变量取值范围是________;
的自变量取值范围是________;
(2)下表是x与y的几组对应值:
x | … | -3 | -2 | -1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | - | -2 | - | - |
|
| 2 |
| m | … |
则表中m的值为________;
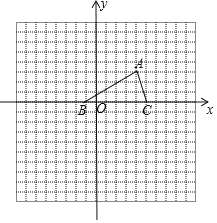
(3)根据表中数据,在如图所示平面直角坐标xOy中描点,并画出函数的一部分,请画出
(4)观察函数图象:写出该函数的一条性质
(5)进一步探究发现:函数y=x+![]() 图象与直线y=-2只有一交点,所以方程x+
图象与直线y=-2只有一交点,所以方程x+![]() =-2只有1个实数根,若方程x+
=-2只有1个实数根,若方程x+![]() =k(x<0)有两个不相等的实数根,则k的取值范围是 ________.
=k(x<0)有两个不相等的实数根,则k的取值范围是 ________.