题目内容
1．
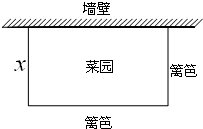如图，要用长40米的篱笆和一面足够长的废弃墙壁围一个矩形菜园（三面用篱笆，一面用废弃墙壁），若垂直墙壁的一面篱笆长为x，菜园的面积为S．（1）写出S关于x的函数解析式；
（2）怎样围才能使菜园的面积最大，最大面积是多少？
分析 （1）先表示出矩形的长，再由矩形的面积公式就可以得出结论；
（2）将（1）的解析式转化为顶点式，由二次函数的性质就可以得出结论．
解答 解：（1）由题意，得
S=x（40-2x），
S=-2x2+40x．
答：S与x之间的函数关系式为S=-2x2+40x；
（2）∵S=-2x2+40x．
∴S=-2（x-10）2+200．
∴a=-2＜0，
∴x=10时，y最大=200．
∴长为：40-2×10=20米．
答：这个矩形的长为20米，宽为10米时，菜园的面积最大，最大面积是200平方米．
点评 本题考查了矩形的面积公式的运用，二次函数的解析式的运用，二次函数的顶点式的运用，解答时求出函数的解析式是关键．
练习册系列答案
相关题目
11．若点A（a，2-a）在第一象限，a为整数，则a的平方根是（ ）
| A． | 1 | B． | ±2 | C． | ±1 | D． | 不确定 |
12．若关于x的方程3x+3a=2的解是正数，则a的取值范围是（ ）
| A． | a≤$\frac{2}{3}$ | B． | a≥$\frac{2}{3}$ | C． | a＞$\frac{2}{3}$ | D． | a＜$\frac{2}{3}$ |
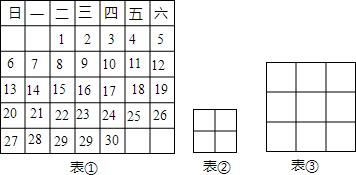
如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF．从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…．