题目内容
已知:a,b是一元二次方程x2+2012x+1=0的两个根,求(2+2013a+a2)(2+2013b+b2)的值.
考点:根与系数的关系,一元二次方程的解
专题:
分析:先由a,b是一元二次方程x2+2012x+1=0的两个根,根据一元二次方程的解的定义得出a2+2012a+1=0,b2+2012b+1=0,于是(2+2013a+a2)(2+2013b+b2)=(1+a)(1+b)=1+(a+b)+ab,再由根与系数的关系得出a+b=-2012,ab=1,代入计算即可求解.
解答:解:∵a,b是一元二次方程x2+2012x+1=0的两个根,
∴a2+2012a+1=0,b2+2012b+1=0,
∴(2+2013a+a2)(2+2013b+b2)
=(1+a)(1+b)
=1+(a+b)+ab,
∵a+b=-2012,ab=1,
∴1+(a+b)+ab=1-2012+1=-2010.
∴(2+2013a+a2)(2+2013b+b2)=-2010.
∴a2+2012a+1=0,b2+2012b+1=0,
∴(2+2013a+a2)(2+2013b+b2)
=(1+a)(1+b)
=1+(a+b)+ab,
∵a+b=-2012,ab=1,
∴1+(a+b)+ab=1-2012+1=-2010.
∴(2+2013a+a2)(2+2013b+b2)=-2010.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.同时考查了一元二次方程的解的定义.
| b |
| a |
| c |
| a |

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
下列各式正确的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
 如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则△OBC的周长为( )
如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则△OBC的周长为( )| A、12cm | B、13cm |
| C、14cm | D、16cm |
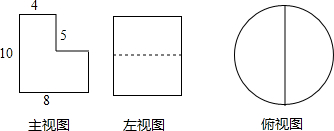 一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.
一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.