题目内容
15．在平面直角坐标系中，四边形ABCD的位置如图所示．
（1）画出四边形A′B′C′D′，使四边形A′B′C′D′与四边形ABCD关于y轴对称，点A′，B′，C′，D′分别为点A、B、C、D的对称点，直接写出点A′，B′，C′，D′的坐标；
（2）画两条线段，线段的端点在四边形ABCD的边上，这两条线段将四边形ABCD分割成三个等腰三角形，直接写出这三个等腰三角形的面积．
分析 （1）分别作出各点关于y轴的对称点，再顺次连接即可得到四边形A′B′C′D′，根据各点在坐标系中的位置写出其坐标即可；
（2）画出符合条件的线段，再判断出△ADE的形状，根据三角形的面积公式即可得出结论．
解答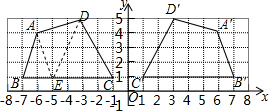 
解：（1）如图所示，A′（6，4），B′（7，1），C′（1，1），D′（3，5）；
（2）如图，线段AE，DE即为所求．
∵AE2=AD2=12+32=10，DE2=22+42=20，
∴AE2+AD2=DE2，
∴△ADE是等腰直角三角形，
∴S△ADE=$\frac{1}{2}$AD•AE=$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$=5，S△ABE=$\frac{1}{2}$×2×3=3；S△CDE=$\frac{1}{2}$×4×4=4．
点评 本题考查的是作图-轴对称变换，熟知关于y轴对称的点的坐标特点是解答此题的关键．
练习册系列答案
相关题目
如图，△ABC三个顶点的坐标分别为A（2，4），B （1，1），C（4，3）．
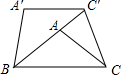如图，将△ABC绕点B逆时针旋转40°，得到△A′B′C′，若点C′恰好落在边BA的延长线上，且A′C′∥BC，连接CC′，则∠ACC′=30度．
7．
把如图所示的平面图形绕直线L旋转一周，得到的立体图形是（ ）
把如图所示的平面图形绕直线L旋转一周，得到的立体图形是（ ）| A． | 圆柱 | B． | 圆锥 | C． | 球 | D． | 棱锥 |
如图，已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，与直线l2：y=-$\frac{1}{2}$x交于点P．直线l3：y=-$\frac{3}{2}$x+4与x轴交于点C，与y轴交于点D，与直线l1交于点Q，与直线l2交于点R．