题目内容
（本题满分7分）已知关于
的方程
．
（1）试说明：无论
取什么实数值，方程总有实数根；
（2）若等腰
的一边长
为1，另两边长
、
恰好是这个方程的两个实数根，求的周长．
（1）证明
，过程略；（2）
【解析】
试题分析：（1）证明一元二次方程总有实根，基本思路是证明
，并利用不等式的性质即可；（2）因题中并未指出哪条边是腰，故需分类讨论，若
，则可根据
求出
进而求出周长，若
或
，则可将
代入方程求出进而求出周长，其中也要注意所求三边长是否能构成三角形.
试题解析：（1）
无论
取何值，方程总有实数根；
（2）①当时，
此时方程化为
解得
，
能组成三角形 
的周长
；
②当或时，把
代入方程，得
，解得
此时方程化为
，解得
，
不能组成三角形，舍
综上，
的周长为
.
考点：1.一元二次方程根的判别式；2.分类讨论；3.三角形三边关系.
练习册系列答案
相关题目
长
，露在水面上的鱼线
长
，某钓鱼者想看看鱼钓上的情况，把鱼竿
的位置，此时露在水面上的鱼线
为
，则鱼竿转过的角度是（ ）.
B．
C．
D．
，
，
，点
是以
为直径的半圆
上一动点，
交直线
于点
，设
．
时，求弧
的长；
时，求线段
的长；
在线段
的延长线上，则
的取值范围是________ _.（直接写出答案）
中，点
是
边的中点，且
//
，则
___________． 
中，直线
经过点
、
，⊙
的半径为2(
是直线
，
为切点，则切线长
B．
C．
D．
，以点B为圆心，BC长为半径画弧，交边AD于点E，若AE·ED＝
，则矩形ABCD的面积为 ．
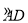的中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD