Question

如图，△ABC内接于⊙O，AB是⊙O的直径，C是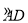的中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD

（1）求证：∠ACH=∠CBD；

（2）求证：P是线段AQ的中点；

（3）若⊙O 的半径为5，BH=8，求CE的长．

Answer 1

（1）证明见解析；（2）证明见解析；（3）8．

【解析】

试题分析：（1）根据垂径定理得出AB垂直平分CE，推出H为CE中点，弧AC=弧AE，根据圆周角定理推出即可．

（2）根据圆周角定理求出∠ACH=∠CAD，推出AP=CP，求出∠PCQ=∠CQP，推出PC=PQ，即可得出答案．

（3）连接OC，根据勾股定理求出CH，根据垂径定理求出即可．

试题解析：（1）证明：∵AB是⊙O的直径，CE⊥AB，

∴AB垂直平分CE，

即H为CE中点，弧AC=弧AE

又∵C是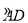的中点，

∴弧AC=弧CD

∴弧AC=弧CD=弧AE

∴∠ACH=∠CBD；

（2）由（1）知，∠ACH=∠CBD，

又∵∠CAD=∠CBD

∴∠ACH=∠CAD，

∴AP=CP

又∵AB是⊙O的直径，

∴∠ACB=∠ADB=90°，

∴∠PCQ=90°﹣∠ACH，∠PQC=∠BQD=90°﹣∠CBD，

∴∠PCQ=∠PQC，

∴PC=PQ，

∴AP=PQ，

即P是线段AQ的中点；

（3）【解析】
连接OC，

∵BH=8，OB=OC=5，

∴OH=3

∴由勾股定理得：CH=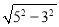=4

由（1）知：CH=EH=4，

∴CE=8．

考点：1．三角形的外接圆与外心；2．勾股定理；垂径定理；3．圆心角、弧、弦的关系．