题目内容
18. 已知二次函数y=ax2+bx+c的图象和x轴有两个交点A、B(点A在点B的右侧),B(-3,0),与y轴的交点为C(0,3)且对称轴是直线x=-1;
已知二次函数y=ax2+bx+c的图象和x轴有两个交点A、B(点A在点B的右侧),B(-3,0),与y轴的交点为C(0,3)且对称轴是直线x=-1;(1)求该二次函数的解析表达式;
(2)在给定的坐标系中画出二次函数草图;
(3)若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
分析 (1)先由抛物线的对称性求得点A的坐标,然后利用待定系数法求解即可;
(2)根据函数的解析式画出函数的图象即可;
(3)如图2所示,过点E作ED⊥AB,垂足为点D,列出四边形的面积与点E的横坐标x之间的函数关系式,利用配方法求得最大值以及点E的横坐标,从而可求得点E的坐标.
解答 解:(1)∵抛物线的对称轴为x=-1,点B的坐标(-3,0),
∴点A的坐标为(1,0).
设抛物线的解析式为y=a(x+3)(x-1),将点C的坐标代入得:-3a=3,
解得;a=-1,
∴抛物线的解析式为y=-x2-2x+3.
(2)二次函数的图象如图1所示: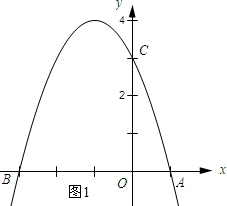
(3)如图2所示,过点E作ED⊥AB,垂足为点D.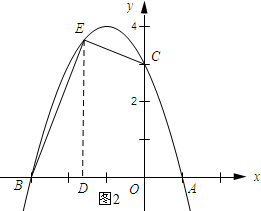
设点E的坐标为(x,-x2-2x+3).
则四边形的BOCE的面积=△BED的面积+梯形EDOC的面积
=$\frac{1}{2}(x+3)(-{x}^{2}-2x+3)$+$\frac{1}{2}×(-{x}^{2}-2x+3+3)×(-x)$
=$-\frac{3}{2}(x+\frac{3}{2})^{2}+\frac{63}{8}$.
∴当x=-$\frac{3}{2}$时,四边形的面积有最大值,最大值面积为$\frac{63}{8}$.
将x=-$\frac{3}{2}$代入y=-x2-2x+3得;y=$\frac{15}{4}$.
∴点E的坐标为($-\frac{3}{2},\frac{15}{4}$).
点评 本题主要考查的是待定系数法求二次函数的解析,配方法求得二次函数的最值,列出四边形的面积与点E的横坐标之间的函数关系式是解题的关键.

练习册系列答案
相关题目
7.下列各对数中,互为相反数的是( )
| A. | -(-2)3与|-2|3 | B. | (-2)3与-23 | C. | -22与+(-2)2 | D. | -(-2)与|-2| |