题目内容
 如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°
如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°(1)若∠AOE=46°,求∠DOB的度数为多少?请你指出与之间的函数关系.
(2)请你指出∠DOB与∠COE之间的数量关系,并说明理由.
考点:角的计算
专题:
分析:(1)由∠DOB=∠AOB-∠AOE-∠DOE,然后将∠AOB=180°,∠AOE=46°,∠DOE=90°代入即可求出∠DOB=44°,根据∠AOE=46°,∠DOB=44°可得∠AOE与∠DOB互为余角;
(2)由OC是∠AOB的平分线,可得∠AOC=90°,因为∠DOE=90°,所以∠AOC=∠DOE,所以∠COE=∠AOD,进而得到∠DOB与∠COE互补.
(2)由OC是∠AOB的平分线,可得∠AOC=90°,因为∠DOE=90°,所以∠AOC=∠DOE,所以∠COE=∠AOD,进而得到∠DOB与∠COE互补.
解答:解:(1)∵∠DOB=∠AOB-∠AOE-∠DOE,∠AOB=180°,∠AOE=46°,∠DOE=90°,
∴∠DOB=180°-46°-90°=44°,
∴∠AOE+∠DOB=46°+44°=90°,
∴∠AOE与∠DOB互为余角;
(2)∠DOB+∠COE=180°,
理由:∵OC是∠AOB的平分线,
∴∠AOC=90°,
∵∠DOE=90°,
∴∠AOC=∠DOE,
∵∠COE=∠AOE+∠AOC
∴∠COE=∠AOE+∠DOE=∠AOD,
∵∠AOD+∠BOD=180°,
∴∠COE+∠BOD=180°.
∴∠DOB=180°-46°-90°=44°,
∴∠AOE+∠DOB=46°+44°=90°,
∴∠AOE与∠DOB互为余角;
(2)∠DOB+∠COE=180°,
理由:∵OC是∠AOB的平分线,
∴∠AOC=90°,
∵∠DOE=90°,
∴∠AOC=∠DOE,
∵∠COE=∠AOE+∠AOC
∴∠COE=∠AOE+∠DOE=∠AOD,
∵∠AOD+∠BOD=180°,
∴∠COE+∠BOD=180°.
点评:此题考查了角的有关计算,解题的关键是:利用两角互余与互补的定义解决问题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
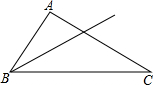 如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )
如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )| A、15° | B、25° |
| C、30° | D、40° |
 如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数.
如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数. 指出如图形所示的数轴上的A、B、C、D、E、F各点分别表示什么数?
指出如图形所示的数轴上的A、B、C、D、E、F各点分别表示什么数?