��Ŀ����
19���ɷ���ļ��㹫ʽs2=$\frac{1}{n}$[��x1-$\overline{x}$��2+��x2-$\overline{x}$��2+��+��xn-$\overline{x}$��2]�����ó�������������ʣ�����1���κ�һ��ʵ���ķ���ǷǸ�ʵ����
����2����һ��ʵ�����ݵķ���Ϊ�㣬��������ݾ���ȣ��Ҷ����ڸ������ݵ�ƽ������
���������������ʺͷ�����㹫ʽ�������������⣺
��֪x+y=2��xy-z2=1����x+y+z��ֵ��
���� �����⣬���������x��y��ƽ��������x��y�ķ�����δ����ú�z�Ĵ���ʽ��ʾ������ɷdz�������2���õ�z��ֵ��0��Ȼ�����x+y+z��
��� �⣺��x+y=2����x��y��ƽ����Ϊ$\frac{x+y}{2}$=1����xy=z2+1
����x��y�ķ���Ϊs2=$\frac{1}{2}$[��x-1��2+��y-1��2]
=$\frac{1}{2}$[x2-2x+1+y2-2y+1]
=$\frac{1}{2}$[x2+2xy+y2-2xy-2��x+y��+2]
=$\frac{1}{2}$[��x+y��2-2xy-2��x+y��+2]
=$\frac{1}{2}$[4-2z2-2-4+2]
=$\frac{1}{2}$[-2z2]
=-z2
��s2��0
��-z2��0��z2��0
��z=0
��x+y+z=2+0=2��
���� ���⿼���˷�������ʣ��������Ĺؼ��ǰ���ֵ����ת��Ϊ�������⣬���÷����������⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
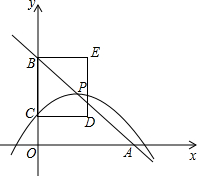 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-x+4��x�ᡢy��ֱ��ڵ�A��B��������y=-$\frac{1}{3}$��x-m��2+n�Ķ���P��ֱ��y=-x+4�ϣ���y�ύ�ڵ�C����P��C�����B�غϣ�����BCΪ��������BCDE����CD=2����P��D��y���ͬ�࣮
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-x+4��x�ᡢy��ֱ��ڵ�A��B��������y=-$\frac{1}{3}$��x-m��2+n�Ķ���P��ֱ��y=-x+4�ϣ���y�ύ�ڵ�C����P��C�����B�غϣ�����BCΪ��������BCDE����CD=2����P��D��y���ͬ�࣮ ��ͼ���ڡ�ABC�У�BPƽ�֡�ABC��CPƽ�֡�ACB����PD��AB��PE��AC��BC=5�����PDE���ܳ���
��ͼ���ڡ�ABC�У�BPƽ�֡�ABC��CPƽ�֡�ACB����PD��AB��PE��AC��BC=5�����PDE���ܳ���