题目内容
12.一颗树苗的高度h(厘米)与测量的年份n满足如下关系:| 年数n | 高度h(厘米) |
| 第1年 | 100 |
| 第2年 | 100+5 |
| 第3年 | 100+10 |
| 第4年 | 100+15 |
(2)求第几年时,树苗高度为130厘米.
分析 (1)根据第1年树苗的高度是100=100+5×(1-1)厘米,第2年树苗的高度是100+5=100+5×(2-1)厘米,第3年树苗的高度是100+10=100+5×(3-1)厘米,第4年树苗的高度是100+15=100+5×(4-1)厘米,…,可得第n年时,树苗的高度h=100+5×(n-1)=95+5n厘米,据此解答即可.
(2)令h=130,根据h=95+5n,求出n的值,即可判断出第几年时,树苗高度为130厘米.
解答 解:(1)因为100=100+5×(1-1),100+5=100+5×(2-1),
100+10=100+5×(3-1),100+15=100+5×(4-1),…,
所以第n年时,树苗的高度是:
h=100+5×(n-1)=95+5n(厘米).
答:第n年时,树苗的高度h是95+5n厘米.
(2)令h=130,则130=95+5n,
所以n=(130-95)÷5
=35÷5
=7(年).
答:第7年时,树苗高度为130厘米.
点评 此题主要考查了探寻数字规律问题,考查了分析推理能力的应用,注意观察总结出规律,并能正确的应用规律,解答此题的关键是判断出:第n年时,树苗的高度是95+5n厘米.

练习册系列答案
相关题目
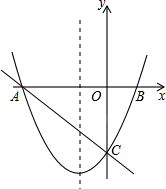 如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.
如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.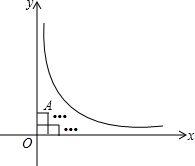 如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.
如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.